[9] 방사성 붕괴
핵공학개론2 2021. 1. 12. 02:27
0. 서론
방사성 원소라 불리는 불안정한 원소는 앞선 글(seraphy.tistory.com/9)에서 설명한 붕괴 현상을 겪으며 더 가벼운, 또는 더 안정한 원소로 변해가는 경향이 있다. 이 과정에서 방사선이 방출되는데, 이 방사선의 강도는 곧 붕괴가 얼마나 일어나는지를 뜻하는 방사능과 같은 의미를 갖는다. 방사성 붕괴는 전체 핵종을 대상으로 일정 확률로 발생하고 이를 붕괴 상수(decay constant)라 한다. 단위 시간당 발생하는 붕괴의 횟수는 전체 핵의 수에 붕괴 확률을 곱한 값으로 결정되며 이를 activity라 부른다.
방사성 원소는 붕괴 과정에서 다양한 원소를 거쳐 간다. 이를 계열(chain)이라 하고, 자연에서 발견되는 대부분의 방사성 원소는 4가지 방사성 계열에 속해 있다. 방사성 물질은 그 양이 지수적으로 감소하는 특성을 가지고 있으며, 간단한 미분방정식을 풀이하면 한 계열 내에서 어떤 방사성 물질이 생성되고 붕괴하는 과정을 수학적으로 확인해볼 수 있다. 이러한 과정은 각 물질의 반감기(붕괴 상수)에 따라 상이한 양상을 보인다.
I. Radioactive Decay
i. 개념
Activity는 단위 시간당 발생하는 방사성 붕괴의 횟수를 의미한다. 단위는 Bq(becquerel)이며, 1Bq는 초당 1회의 붕괴를 나타낸다. 어떤 방사성 핵종이 N개 있을 때, activity A는 다음처럼 쓴다.
$$A = \lambda N$$
이때 λ는 붕괴 상수로, 초당 붕괴 확률을 의미한다. 또한 specific activity는 단위 질량당 activity를 의미하며, 식으로는
$$a = \cfrac{A}{M} = \cfrac{\lambda N}{M} = \cfrac {\lambda N_A}{A} $$
처럼 쓸 수 있다.
붕괴 상수의 역수는 1개의 핵이 붕괴하는 데 걸리는 평균 시간을 의미한다. 이를 decay time이라 하며, τ로 쓴다. 또한 반감기(half-life)는 핵의 수가 붕괴로 인해 절반으로 줄어드는 데 걸리는 시간으로, 다음처럼 계산한다.
$$T_{1/2} = \cfrac{ln2}{\lambda} = 0.693 \tau$$
이는 이하에서 다룰 방사성 원소의 지수적 붕괴 특성을 알면 쉽게 유도할 수 있다.
※ Ci(Curie)
과거에 쓰던 activity의 단위에는 Ci가 있다. 이는
$$1Ci = 3.7 \times 10^{10} Bq$$
로 환산할 수 있으며, 1Ci는 1g의 라듐(Ra-226)의 방사능과 같다. 요컨대 Bq는 매우 작은 단위에 해당한다.
ii. exponential decay
위에서 언급한 붕괴 상수는 단위 시간당 붕괴하는 핵의 개수가 해당 시점의 핵의 수에 비례한다는 사실로부터 유도된다. 식으로는 다음처럼 표현한다.
$$\cfrac{dN}{dt} = - \lambda N$$
이 미분방정식을 풀이하여 activity의 정의에 대입하면 A를 다음처럼 쓸 수 있다.
$$A=A_0 e^{-\lambda t}$$
즉 activity는 지수적으로 감소하는 특성을 가지고 있음을 알 수 있다.
이를 이용해 decay time을 계산해보자. 어떤 핵 하나가 시간 t까지는 붕괴하지 않다가 그 직후 dt 동안 붕괴할 확률은 다음과 같다.
$$t e^{-\lambda t} \lambda dt$$
위 식을 0부터 무한대까지 시간에 대해 적분하여 평균을 내면 다음을 얻는다.
$$\tau = \int_0^{\infty} t\ e^{-\lambda t} \lambda \, dt = \cfrac{1}{\lambda}$$
iii. serial radioactive decay
방사성 물질의 붕괴는 대개 하나의 계열을 따라 순차적으로 이루어진다. 예컨대 3개의 물질 1, 2, 3에 대해, 1에서 2로 변하는 붕괴 상수를 λ_1, 2에서 3으로 가는 붕괴 상수를 λ_2라 하고, 3은 안정하여 더 이상 붕괴하지 않는다고 가정하자. 각 물질의 양을 N_1, N_2, N_3로 두면 다음처럼 식을 세울 수 있다. 1 이외의 핵종은 반응 초기 양이 0이라고 생각한다.

이를 풀이하면 다음을 얻는다. 미분방정식의 풀이 과정은 여기에 적지 않는다.


N_3의 경우 전체 핵의 개수가 보존됨을 이용하여 미분방정식을 풀지 않고도 계산할 수 있다. 이러한 과정을 공식으로 간편히 정리한 것이 Bateman equation이다. 다음의 붕괴에 대해,



각 물질의 양은 다음 식을 따른다. activity는 각 물질의 양에 붕괴 상수를 곱하면 얻을 수 있다.

위 식에서 알 수 있듯이, 방사성 물질의 activity를 결정하는 요인은 물질의 붕괴 상수(또는 반감기)이다. 반감기의 대소 관계에 따라 parent/daughter nuclei 간의 activity 양상이 다르게 나타난다.
a) secular equilibrium
$$when \quad T_1 \gg T_2,$$

1이 거의 붕괴하지 않는 물질이라면, 1의 activity는 거의 일정하게 유지되고 2의 activity는 점차 증가하다가 1의 activity에 수렴하게 된다. 앞서 본 식을 사용해 계산해보면, Bateman equation으로부터 다음을 얻을 수 있다.

1의 반감기가 매우 크다는 것은 반대로 붕괴 상수가 매우 작다는 것이므로, 시간이 충분히 지나면 A_2가 A_1에 근접해 간다는 것을 알 수 있다.
이러한 붕괴 양상은 전체 activity가 초기 상태에 비해 2배로 증가하는 결과를 낳는다. 이는 비단 2개 물질의 관계에서만 나타나는 성질이 아닌데, 만약 방사성 계열의 첫 원소가 매우 느리게 붕괴하고, 이후의 n개 원소가 그보다 매우 빠르게 붕괴하는 특성을 갖고 있다면 이 chain에 의한 activity는 초기 상태에 비해 n+1배까지 증가한다.
b) no equilibrium
$$when \quad T_1 < T_2,$$

1이 2보다 매우 빠르게 붕괴하는 경우, 1이 먼저 붕괴하여 양이 빠르게 감소한 뒤 2만 남아 붕괴가 계속된다. 따라서 전체 activity는 2의 activity로 수렴한다. 2의 양은 1이 붕괴하는 초기에 잠시 증가했다가, 1의 양이 충분히 감소한 뒤에는 점차 감소하는 모습을 보인다.
c) transient equilibrium
$$when \quad T_1 \gtrsim T_2,$$

2의 붕괴가 1보다 조금 더 빠른 경우(이는 (a)에서처럼 너무 많은 차이가 나는 경우를 제외한 모든 경우에 해당한다), 전체 activity가 잠깐 치솟았다가 시간이 지날수록 A_2의 activity가 A_1의 activity로 수렴하는 양상을 보인다.
iv. radioactive chain
자연적인 방사성 원소들은 다음의 4가지 방사성 계열에 속해 있다. 붕괴 과정을 모두 거친 뒤 마지막에는 매우 안정된 원소인 납 또는 비스무트가 된다.


※ 라돈(Rn, Radon)
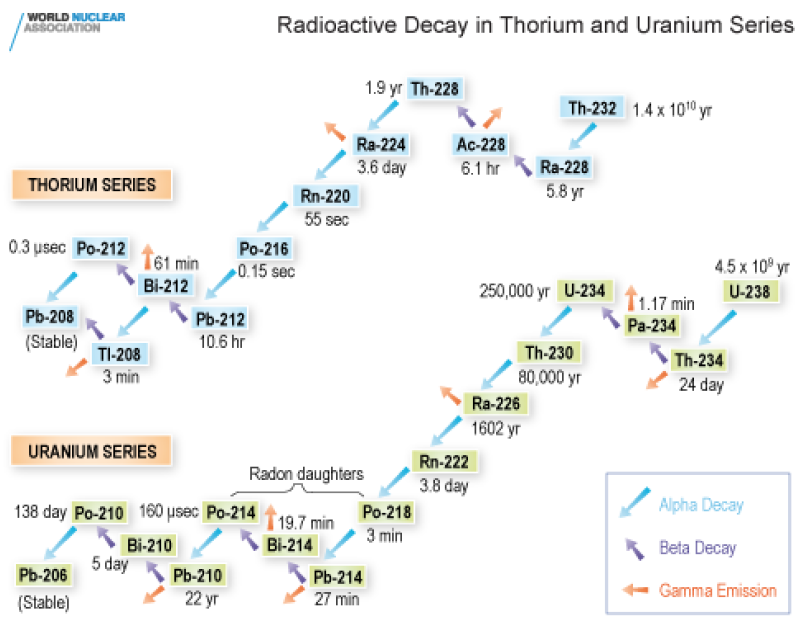
라돈은 우라늄 계열과 토론 계열에 속한 방사성 원소로, 각각 thoron과 radon이라 분류하여 칭하기도 한다. 이것은 원자력 발전에 쓰이는 U나 Pu 같은 연료 물질 다음으로 널리 알려진 방사성 물질 중 하나인데, 예컨대 침대에서 라돈이 검출되었다는 뉴스나 지진을 예측할 방법으로 라돈 가스 검사를 사용한다는 소식 등에서 접할 수 있었을 것이다.
라돈이 다른 원소들과 비교해 갖고 있는 중요한 특성은 상온에서 기체 상태로 존재한다는 점이다. 라돈의 duaghter는 금속이므로, 만약 호흡 과정에서 라돈 가스가 체내에 유입될 경우 금속으로 변한 방사성 물질이 축적될 위험이 있다. 라돈의 붕괴 과정에서 나오는 고에너지의 alpha particle은 공기 중에서 수 cm, 체세포 내에서는 수 mm밖에 진행하지 못해 range가 짧은 편이지만, 체내에 일단 들어오면 초근거리에서 방사선이 나오는 것이므로 심각한 피해를 입을 수 있다. 여기서 그치지 않고 기체로 존재하던 라돈이 붕괴하면 중금속인 납이 되고, 이는 체내에 오랫동안 머물러 있거나 먼지에 흡착되어 돌아다닐 수 있다. 이러한 이유로 라돈은 폐암을 일으키는 등 건강을 위협하는 주요 물질로 알려져 있다.
우라늄 계열의 라돈 가스는 자연에서는 화강암에서, 인공적으로는 인광석으로 제조한 석고에서 주로 방출된다. 자연적으로도 상당한 양이 방출되어 자연방사선량의 대부분을 차지하고, 일부 지역의 토양과 지하수에서는 기준치 이상의 방사능이 측정되기도 한다. 인공적인 경우 시멘트와 콘크리트를 사용한 건물 내에서 검출되기도 한다. 환기를 자주 하는 것만으로 라돈 가스에서 유래하는 위험을 많이 줄일 수 있으나, 라돈 자체가 무거운 원소이기 때문에 저지대, 주택의 지하실, 또는 도시의 지하철역 등에서는 가스가 누적되어 높은 수치의 라돈이 검출되는 일도 발생하고는 한다.
참고문헌
1. A. Beiser, "Concepts of Modern Physics", 6th ed., McGraw-Hill Ltd. (2003)
2. J. Shultis and R. Faw, "Fundamentals of Nuclear Science and Engineering", CRC Press (2016)
3. J. Turner, "Atoms, Radiation, and Radiation Protection", Wiley (2007)
4. Kyoung Jae Chung, "Radioactive Decay(Introduction to Nuclear Engineering)", Seoul National University (2020)
'핵공학개론2' 카테고리의 다른 글
| [11] 광자 (0) | 2021.01.22 |
|---|---|
| [10] 대전 입자 (0) | 2021.01.14 |
| [8] 방사선 기초 (0) | 2021.01.10 |
| [7] 핵융합 기술 (0) | 2021.01.02 |
| [6] 핵융합 기초 (0) | 2020.12.29 |








