[8] 방사선 기초
핵공학개론2 2021. 1. 10. 20:37
0. 서론
Radiation(복사, 또는 방사선)이란 물질이나 에너지가 공간을 통해 전달되는 것을 의미한다. 다만 이 정의만으로는 단순한 수송(transportation)과 구별이 가지 않아, 일반적으로 방사선을 논할 때는 핵에서 물질이나 에너지가 방출되는 것을 뜻하는 방사능(radioactivity)이라는 단어를 같이 사용한다. 요컨대 방사선은 핵반응의 결과로 전자기파의 형태, 또는 에너지를 가진 입자의 형태로 방출되는 에너지를 통칭한다. 우리는 주변에서 방사선과 방사능에 대한 수많은 이야기를 들을 수 있으며, 살아가는 과정 속에서 이러한 원리가 적용된 기술의 혜택을 누리고 있다.

이전의 글(1~7)에서는 플라즈마와 플라즈마를 사용한 핵융합을 주제로 논하였다. 이제부터는 핵공학의 다른 갈래인 방사선을 주제로 다룬다. 방사선은 기본적으로 에너지가 전달되는 한 형태이며, 자주 들어볼 수 있는 X선, 감마선 등의 것도 이 정의를 벗어나지 않는다. 방사선을 이루는 입자, 또는 에너지에 대해 알아봄으로써, 방사선의 활용을 통해 얻을 수 있는 이점과 이로 인해 발생할 수 있는 부작용에 대해 이해할 수 있을 것이다.
I. Radiation의 발생
i. Atomic Structure
Bohr는 1913년, Rutherford가 제시한 '태양계 모형'을 수정하여 최초의 양자화된(quantized) 원자 모형을 제안하였다. Rutherford의 원자 모형은 원자의 중심에 원자의 질량 대부분과 양(+)의 전하를 보유한 원자핵이 있고, 이것을 중심으로 한 원형 궤도를 음(-)의 전하를 가진 전자가 도는 형태로 구성되어 있었다. 태양계에 비유되는 이 모형은 전자가 원운동을 하면서 에너지를 점차 잃다가 결국에는 원자핵에 충돌, 결합하게 된다는 문제점을 가지고 있었다. 만약 원자가 그렇게 이루어져 있었다면, 우주의 모든 물질은 진작에 붕괴되었을 것이었다.
Bohr는 다음의 2가지 가설을 설정하여 이 문제를 해결하고자 했다. 첫째는 전자가 돌 수 있는 원자 주위의 궤도는 이산적으로 정해져 있으며, 이 궤도를 돌고 있는 한 에너지의 손실이 발생하지 않는다는 것, 둘째는 궤도와 궤도 사이에서 전자가 전이할 때 에너지를 방출 또는 흡수한다는 것이었다. Bohr의 모형은 이후 양자역학의 발전에 따라 수정되었지만, 양성자와 전자 1개씩으로 구성된 수소 원자의 특성을 아주 잘 설명할 수 있었다.

Bohr 모형에서 전자가 도는 원형 궤도는 다음의 식에 의해 결정된다(물질파를 사용하면 보다 간단히 서술할 수 있지만, 이는 Bohr 모형이 나온 뒤 11년이 지나 De Brogile에 의해 제안된 것이다).
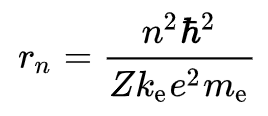
여기서 n은 자연수로, 주양자수라 부른다. 전자 궤도의 반지름은 주양자수 n이 증가함에 따라 그의 제곱에 비례하여 증가한다. 이 궤도들은 원자핵에서 무한히 떨어진 지점에서의 전기 퍼텐셜 에너지를 0이라 둘 때, 마찬가지로 n에 의해 결정되는 에너지 준위를 갖는다. 수소 원자를 기준으로 할 때 이는 다음과 같다.
$$E_n=-\cfrac{13.6eV}{n^2}$$
앞서 전자는 궤도와 궤도 사이에서 전이(transition)할 때만 에너지를 흡수 또는 방출한다고 언급한 바 있다. 전이에서 얻어지는 에너지량은 위 식에 나타난 에너지 준위의 차와 같고, 이는 전자기파의 형태로 나타난다. 그런데 에너지 준위가 주양자수 n에 의해 양자화되어 있으므로, 전이 과정에서 방출되는 전자기파의 에너지 역시 양자화되어 있다(양자화란 단순히 불연속적인 것이 아닌, 이와 같이 특정한 값만을 가질 수 있도록 제한되어 있는 것을 의미한다). 따라서 방출되는 전자기파의 에너지를 측정하면 역으로 어떤 전이가 발생했는지 알 수 있다. 이러한 특성 때문에 높은 준위의 전자가 낮은 준위로 전이하는 과정에서 방출되는 전자기파를 characteristic X-ray라 부른다.
Bohr의 모형은 수소 원자의 특성을 설명하는 데에는 성공했으나, 다전자 원자를 대상으로 한 분석은 잘 맞지 않았다. 이후 Heisenberg, De Brogile, Schrödinger 등에 의해 원자 모형은 현대의 이론과 같게 수정되었다. 양자화된 전자 궤도는 파동함수에 의해 계산되는 전자껍질로 바뀌었고, Schrödinger equation을 따라 전이에 몇 가지 제한이 추가되었다. 다음 그림은 현대의 원자 모형을 간략히 보여주고 있다. 이산적 특성을 함의한 양자수는 주양자수, 궤도 양자수, 자기 양자수, 스핀 양자수 등으로 나뉘어졌고, 이는 아래와 같은 에너지 준위와 전이 규칙(실선은 허용된 전이, 점선은 금지된 전이를 의미한다)으로써 나타난다.

이후의 '핵공학개론2' 태그의 글에서는 원자 모형과 관련된 고전역학적/양자역학적 해석에 대해 이 이상으로 깊게 다루지 않는다. 다만 전자가 서로 다른 에너지 준위 사이를 오가는 과정에서 양자화된 에너지가 전자기파의 형태로 방출 혹은 흡수된다는 점, 그리고 이 때문에 특정 에너지를 갖는 전자기파는 그 에너지량에 해당하는 전이의 확률을 높인다는 점을 알아두자(불확정성 원리). 예컨대 약 12.1eV의 에너지를 가진 광자(photon)가 원자에 진입하면, 12.1eV만큼 높은 에너지 준위로 가는 전이(n = 2 → n = 3)가 발생할 확률이 높다.
ii. Bremsstrahlung Radiation, Auger Effect
원자핵 주위를 지나가는 전자는 전자기력에 의해 속도가 변한다. 이 과정에서 잃은 에너지는 복사의 형태로 방출되고, 이것을 bremssstrahlung radiation이라 한다. 이는 독일어에 기원을 둔 단어로 제동 복사라는 뜻이다. 고속의 전자는 X선을 방출한다.
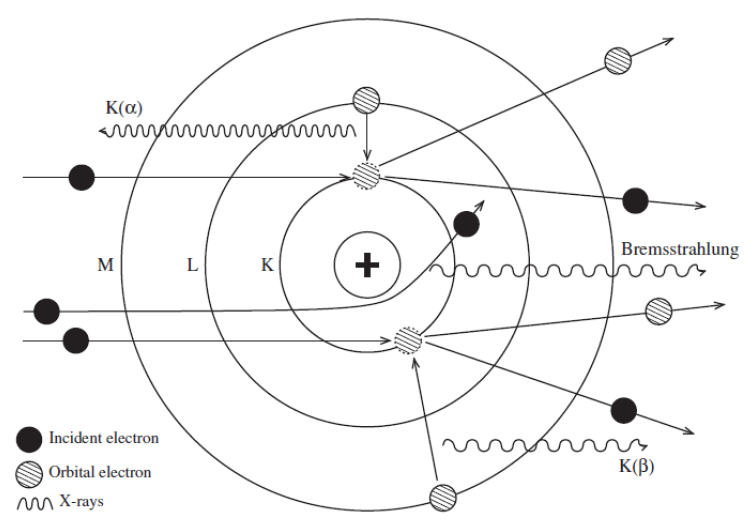
그런데, 이렇게 들어오는 전자 중에는 원자 내 전자에 에너지를 전달하여 이온화를 유도하는 전자가 있을 수 있다. 이렇게 되면 상위 에너지 준위의 전자가 그 빈 자리를 채우기 위해 내려오게 되고, 이 과정에서 그 간격에 해당하는 에너지가 characteristic X-ray의 형태로 방출된다. 따라서 대전 입자가 원자 주위를 지날 때, 연속적인 Bremsstrahlung radiation과 이산적인 characteristic radiation이 모두 관측된다.

전자가 높은 준위에서 낮은 준위로 내려올 때 방출된 전자기파는 또 다른 이온화 반응을 유발하기도 한다. 이로 인해 전자의 전이가 발생하는 동시에 전자가 원자 밖으로 방출되는 현상이 발생할 수 있는데, 이를 Auger effect라 한다.

II. Radiation Energy
일전에 핵융합 관련 글에서 설명한 바와 같이, 핵에너지의 근원은 질량결손이다. 방사성 물질의 붕괴 과정에서 발생하는 방사선도 마찬가지로 손실된 질량에 따라 그 에너지량이 결정된다.
i. 용어 정리
a) nucleus, nucleon, nuclide, element
순서대로 번역하면 핵, 핵자, 핵종, 원소이다. 핵자는 핵을 이루는 입자인 양성자와 중성자를 지칭하고, 핵종은 양성자와 중성자의 수에 의해 구분되는 원자핵(또는 원자)의 종류를 의미한다.
b) isotope, isotone, isobar, isomer
순서대로 동위원소, 동중성자원소, 동중원소, 이성질체를 의미한다. 양성자의 수가 같으나 중성자의 수가 다르면 동위원소, 그 반대의 관계이면 동중성자원소라 한다. 질량수(양성자 수와 중성자 수의 합)가 같은 원소를 동중원소라 하며, 이성질체는 화학에서는 분자식이 같으나 구조가 다른 물질을, 핵공학에서는 에너지 준위가 다른 같은 종류의 핵(동질이성핵)을 말한다.
ii. binding energy
a) AMU
원자의 질량은 일상적인 단위로 표현하기에 너무 작아 새로운 단위가 필요하다. amu(atomic mass unit)는 양성자와 중성자 하나의 질량을 1amu로 설정한 단위이다. 정확히는 탄소 원자
$${}_{\ \ 6}^{12}C$$
의 질량을 12amu로 설정하였다. 1mol이 모이면 12g이 되므로, 1amu는 다음과 같이 변환된다.
$$1AMU = \cfrac{1g}{6.02 \times 10^{23}} = 1.66 \times 10^{24} g$$
핵공학에서는 질량을 에너지 단위로 자주 표현한다. 이에 맞춰 c^2을 곱해 단위 변환을 해주면 다음을 얻는다.
$$1AMU = 931.494MeV$$
b) binding energy calculation
핵의 결합에너지는 각각의 핵자를 따로 놓았을 때의 질량과 합쳐져 있을 때의 질량의 차이와 같다. 요컨대 질량결손이 결합에너지로 변환되는 것이다. 다음은 amu 단위로 표현된 질량결손을 에너지로 변환하는 식을 나타낸 것이다. Z와 N은 각각 양성자와 중성자의 수를, m(A)는 원자 A의 질량(핵과 전자의 질량)을 의미한다. u는 AMU를 나타내는 표기이다.
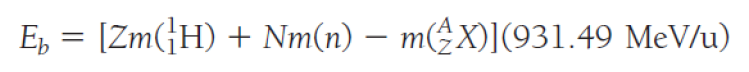
손실된 질량에 따른 에너지를 계산할 때 mass excess(혹은 mass difference)를 사용하기도 한다. 다음 표를 보자.

표 오른쪽의 값들은 원자의 실제 질량(AMU)에서 질량수를 뺀 것을 MeV 단위로 환산한 것이다. 이 표를 활용하면 실제 질량을 사용한 계산보다 간단하게 에너지량을 알아낼 수 있다. 요컨대 atomic mass에 해당하는 항을 mass difference로 그대로 바꿔주면 에너지량을 산출할 수 있다는 것인데, 다음 문단에서 그 예시를 보일 것이다. 결과적으로는 위에 적힌 binding energy의 식의 앞부분

의 계산을 미리 해두는 것과 같다.
iii. Types of Decay
불완전한 방사성 원소는 여러 가지 붕괴 방식을 통해 불안정성을 해소하려는 경향이 있다. 다음은 방사성 붕괴의 몇 가지 유형을 나타낸 것이며, 이외에도 gamma decay, internal conversion 등의 반응이 있다. 이하의 문단에서는 이러한 방사성 붕괴에 대해 알아보고, 여기에서 방출되는 에너지량을 계산하는 방법에 대해 설명하고자 한다.


a) alpha decay(알파 붕괴)
alpha decay는 다음과 같이 alpha-particle을 방출하며 이루어지는 방사성 붕괴 과정이다. 처음에는 방출되는 입자의 정체를 알지 못해 이 방사선을 alpha-ray라고 명명하였으나(다른 방사선의 이름도 비슷한 맥락에서 붙여졌다. beta-ray, gamma-ray 등등), 이후 실험을 통해 헬륨의 원자핵임이 밝혀졌다. 붕괴 과정에서 방출된 이 원자핵은 주위에서 전자를 얻으며 중성화된다.
전하량과 질량수가 보존되기 때문에, 아래와 같은 식으로 표현할 수 있다.

alpha decay는 무거운 핵종(질량수 52 이상)에서만 발생한다. 이전의 글(seraphy.tistory.com/7)에서 binding energy curve를 설명할 때, 양성자와 중성자는 2개씩 pair를 이루어 총 4개가 한 몸으로 움직이려는 경향이 있음을 언급한 바 있다. 이것은 곧 alpha-particle과 같은데, 요컨대 질량수가 큰 핵종에 대해서는 핵반응의 단위가 alpha-particle이 되는 것으로 이해할 수 있다.
alpha decay 과정에서 방출되는 에너지량을 계산해보자. 라듐의 alpha decay는 다음 식으로 표현된다.

질량손실을 계산하면, 에너지량 Q는 다음과 같다.

여기서 대문자 M은 핵의 질량을 나타낸 것이다. 위에서 말한 mass difference를 사용해 이를 계산하려면, 핵의 질량에 전자의 질량을 더한 atomic mass로 값을 바꿔줄 필요가 있다. 위 식에서는 반응 전과 반응 후의 양성자 수가 같으므로, 전자의 수 역시 같다. 따라서 라듐의 핵 질량을 원자 질량으로 바꿀 때 더해지는 88개의 전자 질량은 라돈과 헬륨 원자핵의 질량을 원자 질량으로 바꿀 때 빼야 하는 86개, 2개의 전자 질량에 의해 상쇄되고, Q에 대한 위 식에서 핵의 질량 M은 atomic mass로 곧장 치환될 수 있다. 결론적으로 Q value를 구하는 위 식은 아래처럼 변하고,

이는 모든 형태의 alpha decay에 공통적으로 적용된다.

이때 alpha-particle이 가지게 되는 에너지량은 반응 후 입자들의 질량비로부터 얻을 수 있다. 질량의 역수비로 Q를 나누어 갖게 되므로, 헬륨 원자핵으로 가는 에너지는 다음과 같다. M은 daughter nuclei의 질량, m은 alpha-particle의 질량이다.

앞서 alpha decay는 무거운 핵종에서 발생한다고 설명하였다. 이 때문에 alpha particle은 parent/daughter nuclei에 비해 매우 가벼운 축에 속하며, 그 결과 핵반응에서 얻어지는 에너지의 대부분을 alpha particle이 보유하게 된다.
b) beta decay(베타 붕괴)
beta decay는 중성자가 양성자로 변하는 과정에서 전자를 방출하는 반응이다. 이는 양성자와 중성자 수의 비가 균형이 맞지 않을 때 확률적으로 발생한다.

그런데 위 반응식을 예상했던 이전의 과학자들은 beta decay를 설명하는 데 어려움을 겪었다. 만약 beta decay가 정말 저렇게 이루어진다면, 에너지도, 선운동량도, 각운동량도 보존되지 않을 것이기 때문이다. 측정된 전자의 에너지는 연속적인 분포를 보였고(이는 alpha decay와 비교했을 때 결정적인 차이이다), 핵보다 훨씬 가벼운 전자가 반응에서 나온 거의 모든 에너지를 가지고 있어야 했음에도 그런 일은 거의 일어나지 않았다. daughter nuclei와 전자의 충돌 후 진행 방향은 평행하지 않았으며 중성자, 양성자, 전자의 스핀은 모두 1/2이므로 각운동량도 보존되지 않는다.
언급된 연속적인 운동에너지 분포는 2체 붕괴에서는 발생하지 않는다. 그러므로 3체 붕괴 모델이 예상되었고, 기존의 모델에서 빠진 입자에 대한 논의가 이루어졌다. 1930년 Pauli는 전하량이 0, 스핀이 1/2이고 질량이 없는 입자인 neutrino(중성미자, 처음에는 neutron이라 명명하였으나 Chadwick이 1932년 중성자를 발견하면서 이름이 겹친 관계로 차후 neutrino라 부르게 되었다)의 개념을 제시하였고, 1933년 Fermi는 anti-neutrino(반중성미자)가 추가된 다음의 beta decay 과정을 제안하였다.


neutrino의 실험적인 발견은 1956년 Cowan–Reines neutrino experiment에서 이루어진다. neutrino가 아주 작은, 하지만 분명한 실제 질량을 갖고 있다는 것은 1998년 Super-Kamiokande experiment를 통해 밝혀진다.
이제 코발트(Co)의 예를 들어 beta decay 과정에서 방출되는 에너지량을 계산해보자.

alpha decay에서 했던 것처럼 질량의 변화를 계산한다. 반응 후에 전자가 하나 있으므로 이를 포함한다.
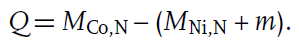
atomic mass로 변환하기 위해, Co에는 전자 27개의 질량을, Ni에는 전자 28개의 질량을 더할 필요가 있다. 이때 Ni에는 이미 1개의 전자 질량이 더해져 있으므로, 마찬가지로 전자 27개에 해당하는 질량이 상쇄된다. 따라서 beta decay에서 얻을 수 있는 에너지량은 parent nuclei(Co)와 daughter nuclei(Ni)의 질량의 차와 같다.

c) gamma decay(감마 붕괴)
원자의 에너지 준위와 유사하게 핵도 에너지 준위를 갖는다. 따라서 '들뜬' 핵이 존재할 수 있으며, 낮은 에너지 준위로 내려갈 때 gamma-ray를 방출한다. 보통 이러한 들뜬 상태는 매우 빠른 시간 내에 끝나는데, 몇몇 핵종은 비교적 긴 시간 동안 들뜬 상태를 유지하며, 이를 metastable state라 한다.
d) electron capture(전자 포획)
beta decay와 반대인 2개의 반응 중 하나가 electron capture이다. 핵의 양성자가 전자를 잡아먹으면서 중성자로 변하고, 중성미자를 방출하는 반응이다.

반응의 결과는 beta decay와 정확히 반대이다. 질량수는 유지되고, 원자번호는 1 감소한다. Pd(팔라듐)의 예시를 들어 살펴보자.

다른 반응과 마찬가지로 반응 전후의 질량 차이로 에너지를 계산하기 전에, 반응 전의 전자가 어느 정도의 에너지를 갖는지 자세히 고려할 필요가 있다. 보통 electron capture에 동원되는 전자는 핵에 가장 가까운 전자껍질인 K-shell에서 온다. 따라서 electron capture가 일어나기 위해서는 질량결손으로 계산한 에너지가 K-shell의 binding energy보다 커야 하고, 또한 Q value를 계산할 때 이 결합에너지를 포함시켜야 한다.
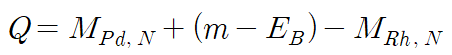
이를 계산하면 다음을 얻는다.

e) positron decay
전자를 흡수하는 electron capture와 달리, positron decay는 전자의 반입자인 양전자(positron)을 방출하는 반응으로 반응 결과는 역시 beta decay의 반대와 같다. 아래 식에는 나타나지 않았으나, beta decay에서 반중성미자가 방출되었던 것과 유사하게 여기서는 중성미자가 함께 방출된다.
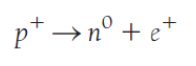
positron decay는 균형 상태에 비해 양성자가 중성자보다 많은 핵종에서 발생하며, electron capture와는 경쟁 관계에 있다. Na의 positron decay를 예로 살펴보자.

Q value를 계산하면,

Na의 전자 수가 Ne보다 1개 많으므로, 전자 1개의 질량을 추가로 빼주어야 atomic mass로 변환할 수 있다. 따라서 다음을 얻는다.
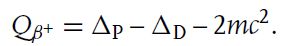
이는 positron decay가 발생하려면 parent/daughter nuclei의 질량 차가 전자 2개의 질량보다 커야 한다는 것을 시사한다. 전자 2개의 질량은 약 1MeV인데, 경쟁 관계의 핵반응인 electron capture의 경우 두 핵의 질량 차가 K-shell의 binding energy보다 커야 한다. 이는 수 keV 수준이므로, electron capture의 Q value가 positron decay의 Q value보다 큰 편이다(즉, 전이 시 에너지 준위의 폭이 넓다). 일반적으로는 positron decay가 일어날 확률이 더 높은 편이다.

f) internal conversion
핵이 들뜬 상태에서 내려올 때 방출되는 에너지는 gamma-ray의 형태로 나오기도 하나, 때때로 전자를 원자 밖으로 내보내기도 한다. 이를 internal conversion이라 하며, 이 과정에서 발생하는 전자의 빈 자리 때문에 characteristic X-ray의 방출, 또는 Auger effect를 동반한다.
참고문헌
1. A. Beiser, "Concepts of Modern Physics", 6th ed., McGraw-Hill Ltd. (2003)
2. J. Shultis and R. Faw, "Fundamentals of Nuclear Science and Engineering", CRC Press (2016)
3. J. Turner, "Atoms, Radiation, and Radiation Protection", Wiley (2007)
4. Kyoung Jae Chung, "Atomic Structure and Atomic Radiation(Introduction to Nuclear Engineering)", Seoul National University (2020)
5. Kyoung Jae Chung, "Nucleus and Nuclear Radiation(Introduction to Nuclear Engineering)", Seoul National University (2020)
'핵공학개론2' 카테고리의 다른 글
| [10] 대전 입자 (0) | 2021.01.14 |
|---|---|
| [9] 방사성 붕괴 (0) | 2021.01.12 |
| [7] 핵융합 기술 (0) | 2021.01.02 |
| [6] 핵융합 기초 (0) | 2020.12.29 |
| [5] 기체 방전 (0) | 2020.12.27 |








