[11] 광자
핵공학개론2 2021. 1. 22. 19:26
0. 서론
α, β선과 달리 γ선은 광자의 형태를 한 방사선이다. 앞선 글(seraphy.tistory.com/11)에서는 대전 입자가 물질과 상호작용하는 과정에서의 stopping power와 range를 계산하였고, 이로부터 에너지와 흡수 물질에 따른 여러 방사선의 정지 양상을 알아보았다. 광자는 이들과 달리 에너지에 따라 변하는 cross-section을 기준으로 광전효과(photoelectric effect), 콤프턴 산란(Compton scattering), 쌍생성(pair production) 등의 반응을 한다. 각 반응이 일어날 확률인 attenuation coefficient를 구하고, 에너지 전달률을 나타내는 energy transfer/absorption coefficient를 구함으로써 광자 형태의 방사선이 가진 에너지가 물질에 전달되는 과정을 살펴볼 수 있다.
I. Interaction
i. Photoelectric Effect
금속의 표면에 빛을 쪼이면 전자가 에너지를 얻어 표면에서 방출되는 현상이 발생한다. 이를 광전 효과라 부르며, 1905년 Einstein이 광양자설을 적용하여 광전 효과를 설명하였다.
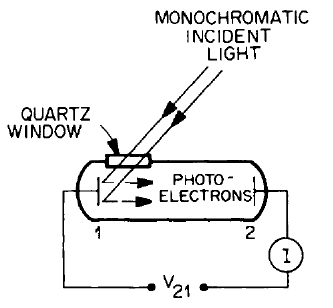
전자가 탈출하는 데 필요한 에너지인 일함수(work function)를 빛의 에너지에서 뺀 값이 전자가 가질 수 있는 최대 운동에너지가 된다. 대개의 경우 광자의 에너지가 일함수에 비해 매우 커 차이를 무시한다.
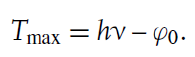
광자가 물질에 부딪힐 때, 광전 효과의 cross-section(attenuation coefficient) τ는 원자번호 Z와 빛의 에너지 ε에 대해 다음처럼 나타난다(아래의 cross-section 기호 중 τ의 왼쪽 아래에 붙은 첨자는 원자 하나를 대상으로 계산한다는 뜻으로 atomic의 첫 글자이다. 만약 첨자가 e인 경우 전자 하나를 대상으로 한다는 의미이다). 간단하게 Z의 4승과 에너지의 -3승에 비례하는 식을 쓰기도 한다.
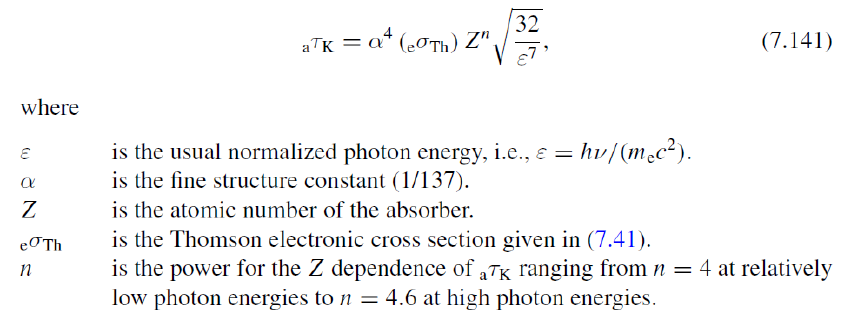
단위길이당, 단위질량당 반응 확률인 mass attenuation coefficient는 다음과 같다.
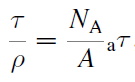
광자의 에너지가 클수록 광전 효과의 발생 확률은 떨어지고, 반대로 원자번호가 커질수록 확률이 증가한다. 아래의 그래프는 광자의 에너지에 대해 나타낸 광전 효과의 atomic cross-section을 보여준다. cross-section은 에너지가 증가함에 따라 점차 감소하는 양상을 보이는데, 간혹 보이는 edge는 전자가 해당 전자껍질(K, L, M, …)에서의 ionization energy 근방의 에너지를 받았을 때 일어나는 확률의 증가를 의미한다.
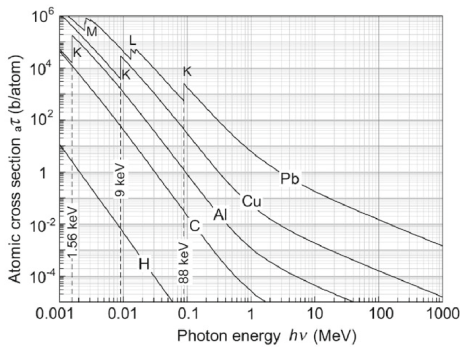
만약 광자의 에너지가 K-shell(핵에 가장 가까운 전자껍질)의 binding energy를 넘어설 경우, 광전 효과에 의해 방출되는 전자의 80% 가량이 K-shell에서 나온다. 이는 K-shell의 전자 밀도가 다른 전자껍질보다 높다는 점에서 기인한다.
ii. Compton Scattering
콤프턴 산란은 광자가 물질과 충돌하여 산란하는 현상을 말하며, 이 과정에서 광자의 에너지 일부가 물질에 전달된다. 다음은 콤프턴 산란이 발생하는 것을 도식화한 것이다.
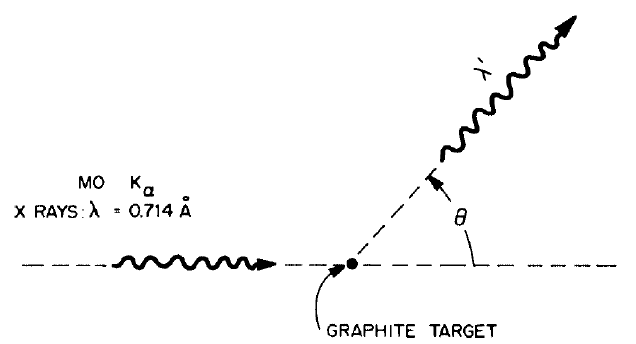
고전적인 전자기학에 따르면, 물질과 광자 사이의 에너지 교환은 없으며(이를 thomson scattering이라 한다) 따라서 산란된 광자의 에너지는 불변한다. 그러나 위 그림의 각 θ마다 빛의 파장에 따른 세기를 측정한 결과는 다음과 같이 2개의 peak를 가진다.
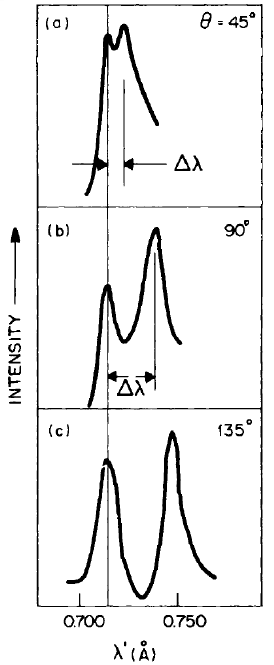
가장 왼쪽의 기준선은 thomson scattering을 거친 빛의 파장이고, 오른쪽에 나타난 peak가 콤프턴 산란에 의해 에너지를 잃은 광자를 의미한다. 이때 산란 후 광자의 에너지와 두 peak 사이의 간격 Δλ는 각각 다음 공식에 의해 계산된다. 이 중 첫 번째 식의 유도 과정은 부록으로 남긴다.
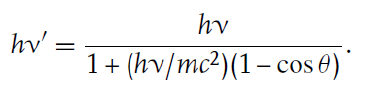
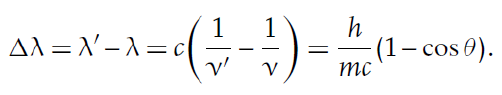
이러한 현상은 1923년 Arthur H. Compton에 의해 이론적으로 설명되었고, 빛의 이중성을 입증하는 사례 중 하나이다.
위 에너지 식에 의하면, 예를 들어 θ=0에서는 thomson scattering에서와 같이 광자가 에너지를 유지하고,
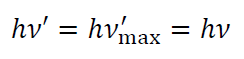
θ=π에서는 광자의 에너지가 최소가 된다. 이는 광자와 충돌한 입자(예컨대 전자)가 얻을 수 있는 에너지의 최댓값이 광자의 본래 에너지에서 전자의 질량 에너지의 절반을 뺀 값이 됨을 보여주기도 한다.
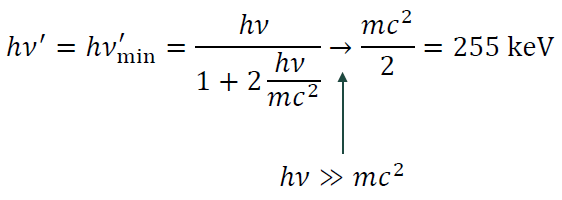
전자 1개에 대한 콤프턴 산란의 cross-section은 Klein-Nishina formula에 의해 다음처럼 결정된다.
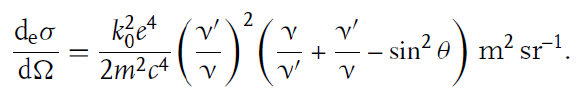
이로부터 scattering angle θ에 따른 cross-section을 계산할 수 있다. 그 결과를 시각화한 것이 다음 그림이다.
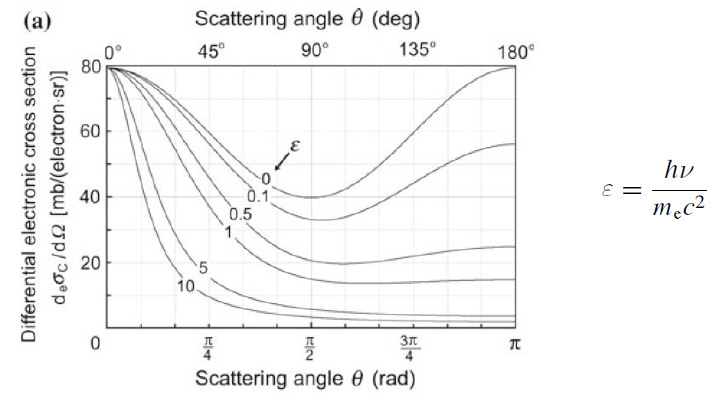
광자의 에너지가 커질수록 대칭성이 사라지고 산란각이 점차 0으로 접근해가는 것을 확인할 수 있다.
모든 cross-section을 각도에 대해 적분하면 콤프턴 산란의 총 cross-section을 얻는다.
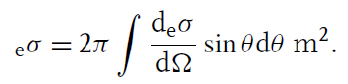
이렇게 구한 콤프턴 산란의 cross-section에 에너지 전달률을 곱해주면 전자 또는 광자가 충돌 후 나눠 갖는 에너지 비율에 대해 가중평균한 cross-section을 구할 수 있다. 전자의 운동에너지를 T라 하면 다음을 얻고,
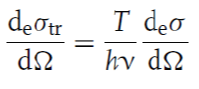
마찬가지로 광자에 대해서도 비슷한 과정을 거쳐 아래의 cross-section을 표현할 수 있다.
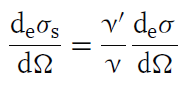
완전 탄성 충돌에서 충돌 후 전자의 운동에너지와 광자의 에너지를 합한 값은 원래 에너지와 같으므로, 위에서 얻은 2개의 cross-section의 합은 콤프턴 산란의 총 cross-section과 같다. 그러므로 이상의 과정으로부터 콤프턴 산란 과정에서 전자가 평균적으로 전달 받는 에너지량을 구할 수 있다. 요컨대 다음의 식에서,
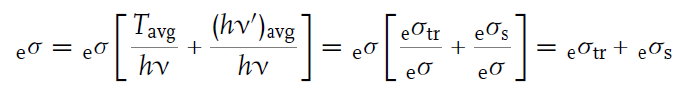
transfer cross-section과 scattering cross-section의 비는 전자와 광자가 평균적으로 갖는 에너지의 비율과 같다.
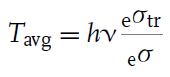
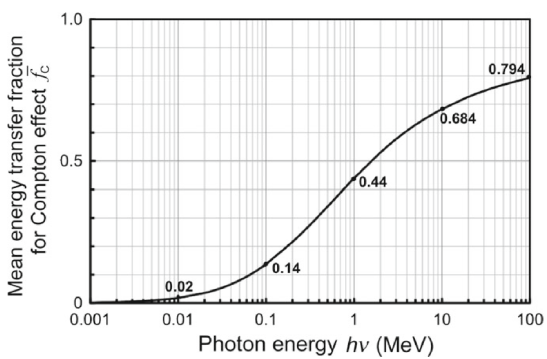
다음 그래프는 광자의 에너지가 증가함에 따라 전자로 전달되는 에너지의 비율이 증가하는 것을 보여준다. 이후에 언급하겠지만, 이것은 낮은 에너지 영역에서의 콤프턴 산란은 transfer보다 scattering 쪽이 잘 일어나기 때문이다.
평균 에너지 전달률이 아닌, 특정 에너지가 전달될 확률을 구하는 것은 다음 공식을 사용하며,
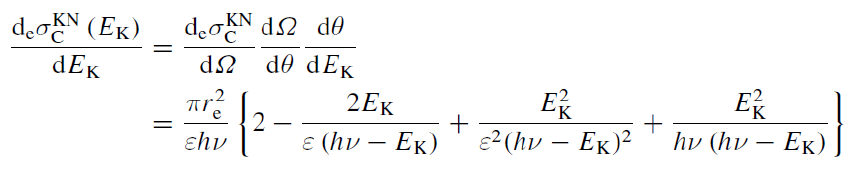
그 값은 다음과 같이 최대 에너지 근방에서 peak를 그리는 형태로 나타난다. 그래프에 나타난 recoil energy(반발에너지, 즉 충돌 후 전자의 운동에너지)의 최댓값은 광자의 back scattering으로 인해 전자가 얻는 최대 에너지와 같다. 아래의 그래프는 광자의 에너지가 1MeV일 때의 데이터이다.
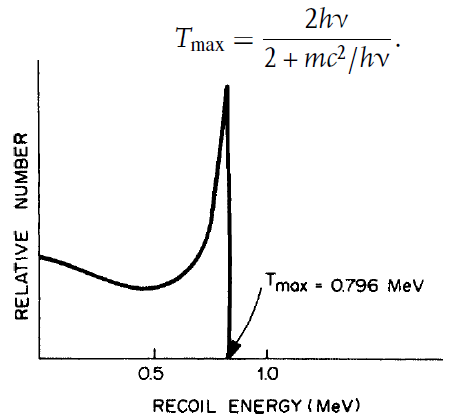
콤프턴 산란의 attenuation coefficient는 앞서 구한 cross-section이 전자 1개에 대한 것이었으므로, 물질의 밀도 N과 해당 물질의 원자번호, 즉 원자가 가진 전자의 수 Z를 위에서 얻은 cross-section에 곱하여 구할 수 있다.
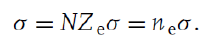
transfer/scattering attenuation coefficient는 앞서 설명한 대로 에너지 전달률을 곱함으로써 계산할 수 있으며, 단위질량당의 attenuation coefficient는 광전 효과 문단에서 쓴 방법과 동일한 과정(밀도로 나누어주는)을 통해 얻을 수 있다.
iii. Pair Production
쌍생성이란 광자가 대전 입자나 다른 광자 주위를 지날 때, 소멸하면서 전자와 양전자를 생성하는 반응을 말한다. 방사선에 의한 쌍생성은 주로 원자의 핵을 대상으로 한 반응을 가리킨다. 전자와 양전자를 새로 만드는 반응이기 때문에, 쌍생성이 일어나기 위해서는 광자의 에너지가 전자 2개의 질량에 해당하는 1.022MeV보다 클 필요가 있다. 초과된 에너지는 전자와 양전자의 운동에너지로 전환되거나 핵에 recoil energy로써 전달된다. 그러나 일반적으로 recoil energy는 계산 시 무시할 수 있다.
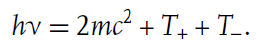
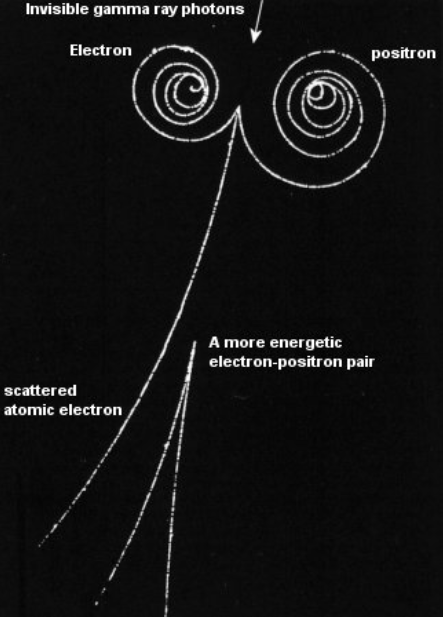
위 사진처럼 핵 이외에도 전자 주위를 지나는 광자가 쌍생성을 일으킬 수도 있다. 이때는 전자가 scatter되면서 총 세 갈래의 입자 궤도가 관측되는데, 이러한 이유로 전자에 의한 쌍생성을 triplet production이라 부르기도 한다. 다만 이 경우 필요한 최소 에너지가 전자 4개의 에너지인 2MeV로 결정되며, 발생 확률도 핵에서의 반응과 비교할 때 현저히 낮은 편이다.
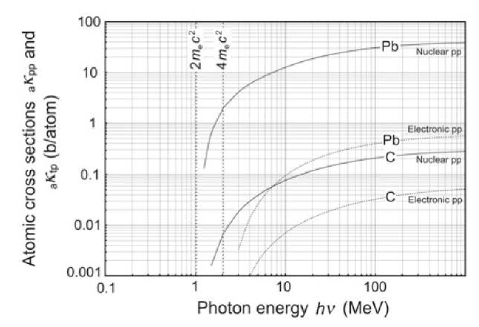
쌍생성의 cross-section κ는 다음처럼 쓰고, 이로부터 cross-section이 원자번호 Z의 제곱에 비례한다는 것을 알 수 있다. 또한 아래의 그래프는 광자의 에너지가 증가할수록 쌍생성 확률도 점차 높아지는 것을 보여준다.
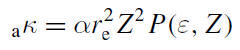
쌍생성으로 인한 에너지 전달률은 생성된 전자와 양전자가 갖는 운동에너지의 비율로 계산한다. 요컨대 평균적으로 전달되는 에너지의 fraction은 다음과 같다.
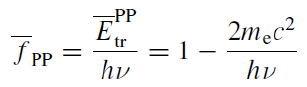
그런데 많은 경우 전자 질량의 2배에 해당하는 에너지보다 광자의 에너지가 매우 크므로, 거의 모든 에너지가 물질로 전달된다고 보아도 무방하다. 따라서 transfer attenuation coefficient는 쌍생성의 cross-section에 원자 밀도를 곱한 값으로 쓸 수 있다.
II. Attenuation Coefficient
위의 논의에서 반응의 확률인 cross-section과 더불어 (linear) attenuation coefficient라는 단어가 계속해서 등장하였다. 이는 incident particle(여기서는 광자)이 단위길이를 나아갈 때마다 물질과 반응할 확률을 말하며, macroscopic cross-section과 같은 의미이다(이에 대해서는 seraphy.tistory.com/2를 참조). 그 값은 광자의 에너지 또는 물질의 특성에 의해 영향을 받는다.
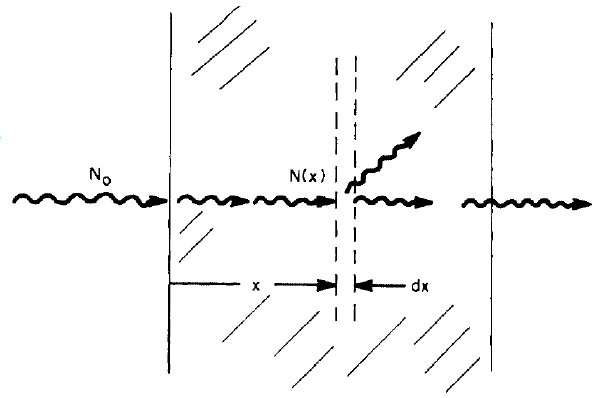
광자와 같이 물질과의 반응이 확률적으로 이루어지는 입자의 경우, 물질 내에서 주파한 거리(depth)에 따라 입자의 수 N은 초기값에서부터 지수적으로 감소한다(방사성 물질의 붕괴와 유사하다. seraphy.tistory.com/10을 참조).
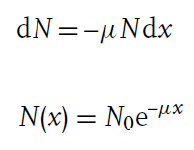
i. Photon
광자는 물질과 만났을 때 광전 효과, 콤프턴 산란, 쌍생성 중 하나의 반응을 한다. 따라서 광자의 attenuation coefficient μ는 다음처럼 쓸 수 있다. 각 반응의 attenuation coefficient는 문자 τ, σ, κ로 쓰는 것이 일반적이며, 오른쪽은 단위질량에 대해 계산한 값인 mass attenuation coefficient이다.
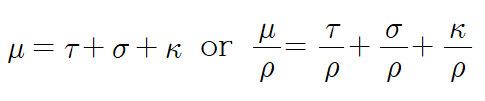
또한 이는 microscopic cross-section에 target(원자)의 밀도를 곱한 값으로도 쓸 수 있다. 단위로 생각해보면 micro는 넓이 단위, macro는 길이의 역수 단위이므로 성립함을 알 수 있다.
다음은 광자의 mass attenuation coefficient를 그래프로 나타낸 것이다.
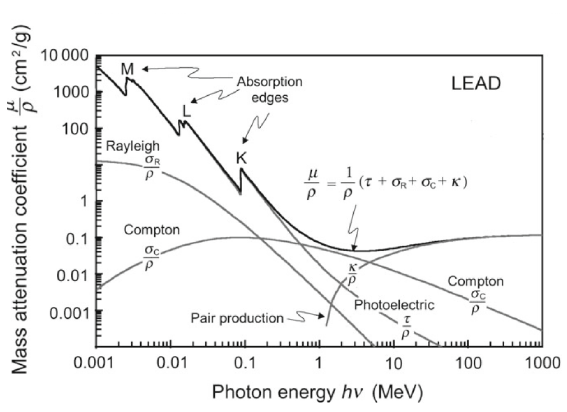
저에너지 구간에서는 광전 효과가, 문턱 에너지(threshold) 이상의 고에너지에서는 쌍생성이 지배적인 반응으로 자리잡으며, 콤프턴 산란은 전체 에너지 영역에서 모두 발생할 수 있음을 확인할 수 있다. 매우 낮은 에너지 영역에서는 Rayleigh scattering이 발생하기도 하는데, 이는 빛의 파장보다 입자의 크기가 훨씬 작을 때 발생하는 탄성 산란을 말한다. 흔히 하늘이 푸른 이유를 설명할 때 등장하는 산란은 Rayleigh scattering을 지칭한다.
ii. Energy Transfer and Absorption
위에서 본 mass attenuation coefficient는 반응 확률을 의미하지, 에너지가 얼마나 전달되는지를 보여주지는 않는다. 따라서 에너지 전달률을 나타내는 energy transfer coefficient를 알기 위해서는 다음처럼 추가로 계산을 해주어야 한다. 이에 대한 설명은 위에서 언급한 바 있으므로 간략하게만 서술하고자 한다.
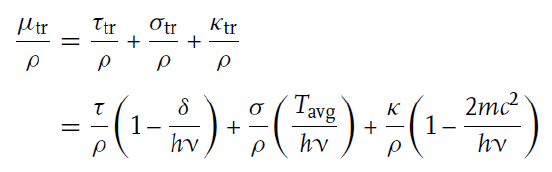
각각의 mass attenuation coefficient에 곱해진 값은 에너지 전달률을 의미한다. 콤프턴 산란에서는 전자의 평균 운동에너지가, 쌍생성에서는 전자와 양전자 생성에 필요한 에너지를 제한 나머지가 전달된다. 그런데 광전 효과의 경우, 위에서는 일함수를 뺀 나머지 에너지가 전자의 운동에너지로 전환된다고 하였으나, 전자가 방출되는 과정에서 발생하는 Auger effect에 의해 어느 정도는 잃은 에너지량을 되찾을 수 있다. Auger effect에 의해 전자가 방출되면 그 에너지는 물질에 전달될 것이고, X선이나 감마선의 형태로 방출되면 손실이 된다. 따라서 위 식처럼 소실되는 에너지의 비율을 δ로 쓰는 것이다.
이렇게 계산한 energy transfer coefficient μ_tr를 mass attenuation coefficient μ로 나누어준 값은 초기에 입사한 광자의 에너지 중 전자의 에너지로 변환되는 비율을 의미한다. 그런데 에너지를 얻은 전자는 bremsstrahlung에 의해 전자기파 형태로 에너지를 잃을 수 있어 그 확률을 마지막에 고려해주어야 한다. 그 비율을 g라 두면, 다음처럼 수정할 수 있다.
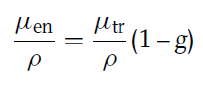
위 식의 μ_en을 energy absorption coefficient라 한다. 아래는 이를 물질 원소별로 나타낸 그래프이다.
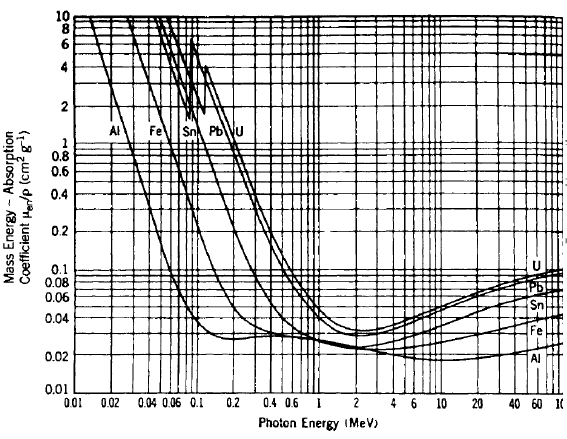
저에너지 영역에서 흡수율이 높다가, 고에너지 영역으로 갈수록 감소세를 보이는 것을 확인할 수 있다. 고에너지 영역에서 주로 발생하는 쌍생성은 광자의 거의 모든 에너지가 물질에 전달되지만, 발생 확률 자체가 낮은 편이어서 실제 흡수율은 그렇게 높지 않다. 또한 원자번호가 클수록 흡수율이 높아지는데, 이러한 경향은 cross-section을 계산할 때 보았던 Z에 비례하는 특성을 기억한다면 어렵지 않게 이해할 수 있다.
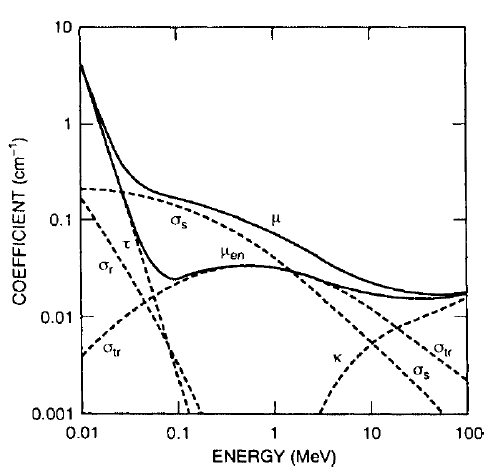
위 그래프는 μ와 μ_en을 비교한 것이다. 두 계수의 차이가 크게 벌어지는 영역은 저에너지 영역의 콤프턴 산란이 발생하는 범위로, 이 범위에서는 scattering이 지배적인 반응으로 등장한다. 콤프턴 산란의 attenuation coefficient를 구성하는 transfer/scattering coefficient 중 scattering의 경우 전자로 에너지가 전달되지 않기 때문에 이러한 차이가 발생한다.
그 외에 무거운 원소일수록 전자의 radiation에 의한 에너지 손실이 증가하므로, transfer coefficient와 absorption coefficient의 차이가 증가하는 경향이 있다. 다음은 이전 글(seraphy.tistory.com/11)에서 소개한 근사식으로, 원자번호가 클수록 radiation의 비중이 커지는 것을 보여준다.
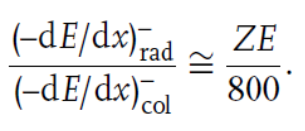
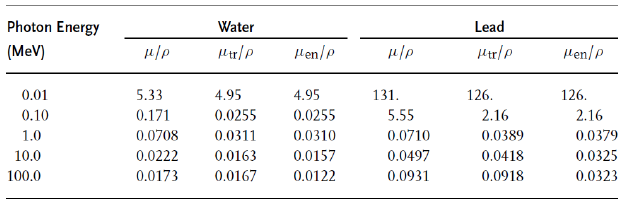
아래 표는 가벼운 분자인 물과 무거운 원자인 납의 attenuation/transfer/absoprtion coefficient를 나타낸 것이다. 물의 경우 transfer coefficient와 absorption coefficient의 차이가 크지 않지만, 납의 경우 100MeV 영역에서 3배까지 차이가 나는 것을 확인할 수 있다.
iii. Limitation
attenuation coefficient를 사용한 이상의 분석은 target의 두께가 attenuation coefficient의 역수로 결정되는 기준 길이보다 얇을 때만 정확하다. 이 조건이 없으면, incident particle의 1차 반응에서 생성된 새로운 입자들이 물질과 또 반응하는 등 예상에서 벗어나는 일이 일어날 수 있어 오차가 발생한다.
부록 : 콤프턴 산란 후 광자의 에너지 유도

참고문헌
1. J. Shultis and R. Faw, "Fundamentals of Nuclear Science and Engineering", CRC Press (2016)
2. J. Turner, "Atoms, Radiation, and Radiation Protection", Wiley (2007)
3. Kyoung Jae Chung, "Interaction of Photons with Matter(Introduction to Nuclear Engineering)", Seoul National University (2020)
'핵공학개론2' 카테고리의 다른 글
| [12] 방사선 노출 (1) | 2021.01.23 |
|---|---|
| [10] 대전 입자 (0) | 2021.01.14 |
| [9] 방사성 붕괴 (0) | 2021.01.12 |
| [8] 방사선 기초 (0) | 2021.01.10 |
| [7] 핵융합 기술 (0) | 2021.01.02 |








