[1] 핵분열 기초
핵공학개론1 2021. 1. 27. 02:21
0. 서론
자연의 모든 물질들은 안정한 상태로 변하려는 성질을 갖는다. 핵의 안정성을 나타내는 지표 중 하나인 핵자당 binding energy를 그래프로 그리면 다음과 같다.

binding energy가 높을수록 안정한 핵이다. 위 그래프를 보면 Fe(철)의 binding energy가 가장 높은 것을 알 수 있는데, 이 때문에 Fe의 좌우에 있는 원소로부터 Fe로의 핵반응이 일어나게 된다. 원자번호가 낮은 H, He 등이 결합하여 더 무거운 핵을 형성하는 반응이 핵융합, U와 같은 물질이 붕괴하여 점차 가벼운 원소로 변하는 것을 핵분열이라 한다. 이 과정에서 총 질량에 손실이 발생하고, 이것은 질량-에너지 등가 원리에 의해 엄청난 양의 핵에너지가 되어 핵반응 도중에 방출된다.
'핵공학개론2' 태그의 글에서는 위 두 가지 반응 중 핵융합을 중점적으로 살펴보았다. 이제부터의 '핵공학개론1' 태그의 글에서는 다른 하나의 반응인 핵분열에 대해 알아보고자 한다. 발전(發電)이 가능할 정도의 상용화가 아직 이루어지지 않은 핵융합과는 달리, 핵분열은 원자력 발전소의 예와 같이 실질적인 에너지원으로써 이미 널리 사용되고 있다. 핵분열이란 간단히 말해 U(우라늄), Pu(플루토늄) 등 무거운 방사성 원소를 원료로 하여, 중성자에 의한 연쇄반응을 일으켜 에너지를 얻는 것이다. 이때 연쇄반응의 속도를 적절히 제어함으로써 시간당 얻을 수 있는 에너지의 양을 조절한다. 이것은 핵분열을 활용한 기술들, 예컨대 소형 원자로부터 원자폭탄까지의 것들에 공통적으로 적용되는 원리이다.
본 글에서는 중성자와 방사성 원소와의 상호작용을 자세히 알아보기 전, 사전에 기억해둘 내용을 간략히 정리하고 핵분열의 전반적인 과정을 개괄적으로 살펴보고자 한다. 다만 일부 내용은 '핵공학개론2' 태그의 일부 글에서 다룬 것과 중복되므로, 해당 글의 링크를 아래에 첨부하니 참고하기를 추천한다.
2020/11/25 - [핵공학개론2] - [1] 플라즈마 개념 정리
2020/12/29 - [핵공학개론2] - [6] 핵융합 기초
2021/01/10 - [핵공학개론2] - [8] 방사선 기초
I. 기본 원리
i. 핵분열
U-235는 방사성 붕괴 원소로, 원자력 발전에 쓰이는 주요 물질 중 하나이다. 붕괴 과정은 다음과 같다.

혼동하지 말아야 할 것은, 핵분열 과정은 이러한 자연적인 붕괴 과정과 다르다는 점이다. 실제 핵분열은 U-235에 중성자를 충돌시킴으로써 일어나고, 다음 그림은 그때 발생할 수 있는 여러 가지 분열 양상 중 하나를 보여준다. 요컨대 U-235의 핵분열 결과로 생성되는 daughter nuclide의 조합은 다양하다.

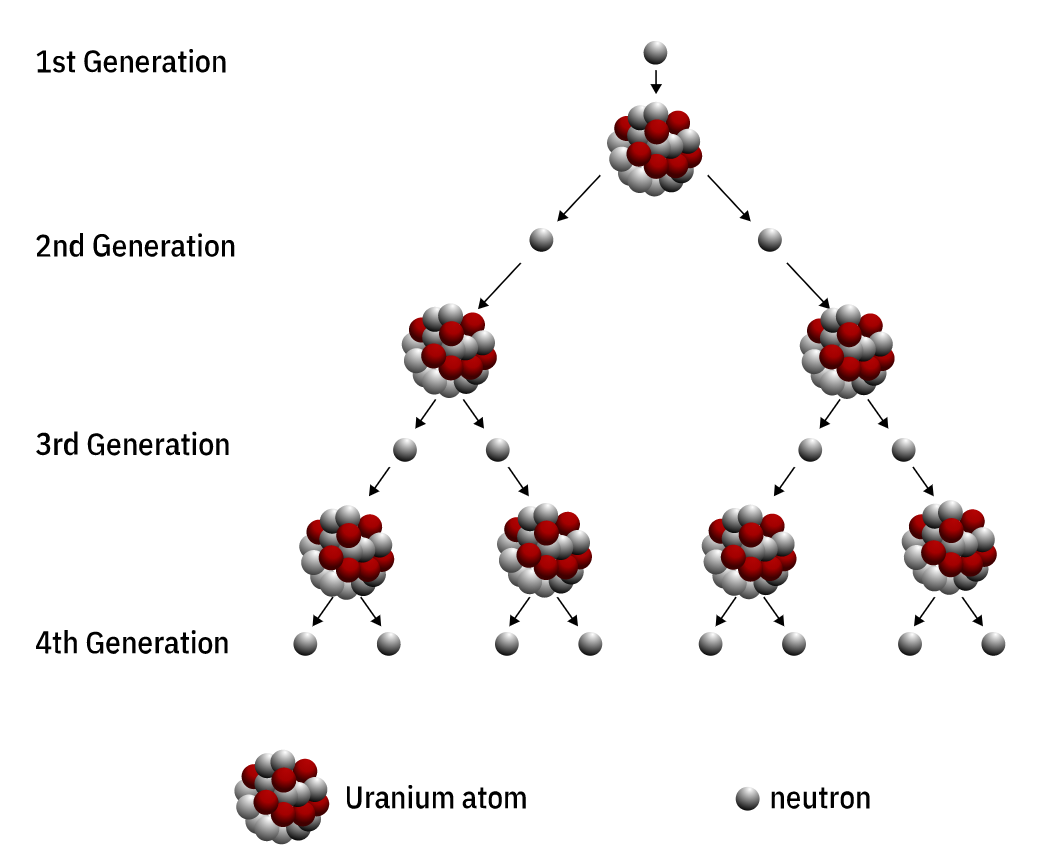
위 그림에서 주목할 점은 중성자 1개를 투입한 결과 새로운 중성자가 2개 만들어졌다는 점이다. 이러한 재생산 덕분에 U-235로 채워진 chamber에 중성자를 입사시키기만 하면, 그 뒤로는 자연스럽게 연쇄반응이 일어나 연료가 바닥날 때까지 핵분열 반응이 이어진다. 다만 유출이나 흡수가 없는 이상적인 상황을 가정할 때, 위 반응을 시작한 뒤 가만히 바라만 본다면 반응당 2배씩 늘어나는 중성자에 의해 방출되는 에너지량이 걷잡을 수 없이 늘어날 것이며, 실험 장소는 곧 대규모의 폭발 현장으로 변하고 말 것이다. 이것은 원자폭탄의 작동 방식과 같다.
원자력 발전과 같은 실제 상황에서는 중성자가 자연적인, 인공적인 여러 요인에 의해 소실된다. chamber 바깥으로 유출될 수도 있고, 연료가 아닌 다른 물질에 흡수될 수도 있으며, 설령 정확한 물질에 충돌한다 해도 원하는 핵반응이 일어나지 않을 수도 있다. 이 모든 것이 중성자의 수를 줄이는 원인이 된다. 따라서 핵분열 반응을 안정된 상태로 유지하고 싶다면 핵반응으로 생성되는 중성자 수와 손실되는 양을 조절하여 증배계수(한 세대(generation)의 중성자 수로 다음 세대의 중성자 수를 나눈 값)가 1이 되도록 할 필요가 있다. 운행 중인 원전은 일반적으로 증배계수가 1인 임계 상태를 유지한다.
ii. 수 밀도(atomic number density)
핵분열 과정의 정량적인 분석을 위해서는 핵연료 내에 담긴 U-235의 양을 알 필요가 있다. 우라늄에는 U-235와 U-238이 있는데, 이 중 핵분열에 주로 사용되는 쪽은 U-235이다. 자연 상태에서 U-235의 비율은 약 0.7% 수준으로 매우 적은 편이다.
핵연료 내 물질의 비율에 대한 정보로는 개수 비와 질량비가 있다. 이를 각각 a와 w로 나타낼 때, 여러 동위원소로 구성된 물질 내에서 특정 동위원소 i와 j의 개수 비 및 질량비 간의 관계는 다음 비례식으로써 주어진다. A는 각 동위원소의 질량수를 나타낸다.

만약 동위원소가 두 종류뿐이라면, 개수 비와 질량비의 총합이 1이라는 점으로부터 다음처럼 쓸 수 있다.

이를 정리하면 아래의 관계식을 얻는다.


이렇게 얻은 비율을 토대로 특정 물질의 수 밀도를 계산할 수 있다. 간단한 예제를 통해 핵연료의 U-235 수 밀도를 계산해보자. 다음은 3w/o의 UO2(Uranium Dioxide, 원자력 발전의 원료로 쓰임)에서 U-235의 밀도를 구하는 과정이다. UO2의 밀도는 10.95g/cm^3이고, 3w/o의 표기는 U-235의 질량비가 3%로 주어진 것을 의미한다.

이처럼 질량비로부터 개수 비를 계산해내면, 물질 내에 포함된 특정 구성원의 밀도를 구할 수 있다.
iii. cross section(반응 단면적)
cross section에 대한 설명은 이전 글(상단 링크 참조)에서 한 번 다룬 바 있다. 면적의 단위를 갖는 것이 microscopic cross section, 길이의 역수 단위를 갖는 것이 macroscopic cross section이었다. macroscopic cross section에 (incident neutron) flux를 곱하면 단위부피당 반응 속도인 reaction rate을 얻는다.

또한 macroscopic cross section의 역수를 mean free path라 하여, incident neutron이 반응 전까지 평균적으로 갈 수 있는 거리를 구할 수 있었다. 이는 아래의 적분을 통해서도 얻을 수 있다. 길이 x까지 반응하지 않다가 그 직후 dx 동안 반응한다고 가정할 때, x의 평균값은 다음과 같이 계산한다.

마지막으로 방향성을 갖는 flux인 angular flux에 대해 알아보자. 입체각 Ω의 근방 dΩ에서 움직이는 중성자의 밀도를 n(Ω)dΩ라 할 때, 같은 근방에서의 중성자 세기(intensity)는 다음처럼 쓰고,

이로부터 angular flux를 얻는다. 이 경우 scalar flux와는 달리, angular flux에 미소입체각 dΩ를 곱해야만 유의미한 값인 intensity(단위면적당, 단위시간당 입사하는 중성자 수)를 얻을 수 있음을 기억해야 한다.

참고문헌
1. Han gyu Joo, "Fundamentals of Nuclear Reaction(Introduction to Nuclear Engineering 1)", Seoul National University (2020)
2. J. K. Shultis, R. E. Faw, "Fundamentals of Nuclear Science and Engineering", 2nd ed., CRC Press (2008)
3. J. R. Lamarsh, A. J. Baratta, "Introduction to Nuclear Engineering", 3rd ed., Prentice Hall (2001)
4. 이은철, 조건우, 김응수, "핵공학개론", 한티미디어 (2018)
이미지
1. metadata.berkeley.edu/nuclear-forensics/Decay%20Chains.html
2. www.iaea.org/newscenter/news/tackling-the-challenges-of-nuclear-data-in-the-future
3. www.atomicarchive.com/science/fission/chain-reactions.html
'핵공학개론1' 카테고리의 다른 글
| [6] 열역학 기초 (0) | 2021.03.15 |
|---|---|
| [5] 원자로 내 중성자 분포 (1) | 2021.02.16 |
| [4] 4인자 공식(Four Factor Formula) (0) | 2021.02.12 |
| [3] 에너지에 따른 중성자 분포 (1) | 2021.02.07 |
| [2] 중성자 (0) | 2021.01.31 |








