[4] 4인자 공식(Four Factor Formula)
핵공학개론1 2021. 2. 12. 22:04
0. 서론
지지난 글(seraphy.tistory.com/15)의 마지막에서 재생계수(reproduction factor)에 대한 내용을, 지난 글(seraphy.tistory.com/16)에서는 증배계수(multiplication factor)에 대한 내용을 언급한 바 있다. 원자로에서 지속적인 핵분열 반응이 일어나도록 하기 위해서는 중성자가 원활히 공급되는 것이 중요하다. 일반적으로 핵분열 과정에서는 투입된 중성자보다 방출되는 중성자가 더 많은데, 여기서 유실이나 흡수 등의 이유로 손실되는 양을 뺀 나머지가 초기 수량보다 많으면 연쇄반응을 통해 원자로를 계속 가동할 수 있다.
핵연료에서 생성된 중성자는 감속 과정에서 resonance에 의해 핵연료에 흡수되기도 하고, 감속재에 흡수되기도 한다. 감속을 마친 열중성자는 absorption/fission cross section에 의해 결정되는 reproduction factor에 따라 새로운 중성자를 만들어내는 데 쓰이고, 이렇게 생성된 중성자는 고에너지 영역에서의 반응까지 거쳐 다음 세대로 넘어간다. 이러한 각각의 과정에서 발생하는 중성자 수의 증감 비율을 모두 곱하면 주기당 배율이 되는데, 그 값을 증배계수라 부른다. 본 글에서는 지난 글에서 짧게 설명한 것에 더해 증배계수에 대한 논의를 보충하고, 이를 구성하는 4인자에 대해 살펴보고자 한다.
I. Infinite Multiplication Factor(무한증배계수)
무한증배계수는 증배계수를 계산할 때 cell의 부피가 무한대라고 가정하고 구한 값을 말한다. 이러한 가정을 통해 클래딩의 부피와 중성자의 누설을 무시할 수 있다. Cell 내부의 fuel에서는 fission과 absorption이 발생하고, moderator에서는 absorption만 발생한다.
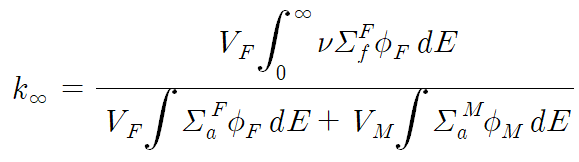
지난 글에서 중성자의 에너지에 따라 thermal, epithermal, fast로 영역을 구분하였고, 각 영역에서의 중성자 flux에 따라 cross section을 가중평균하는 과정을 살펴보았다. 이후의 macroscopic cross section은 따로 언급하지 않으면 가중평균된 값을 의미한다.
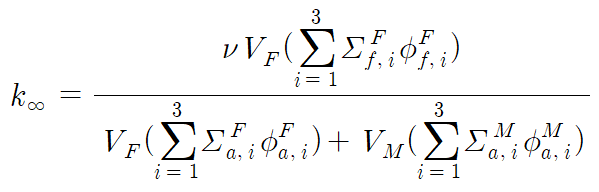
i. 근사
이제 위 식을 근사하여 등장하는 항을 일부 소거해보자. 지난 글에서의 표기에 따르면 에너지가 낮은 순서대로 1, 2, 3의 우하첨자를 사용하기로 하였다. Absorption은 낮은 에너지의 중성자에 대해 주로 일어나므로 고에너지 영역에서의 반응은 비율이 적어 무시할 수 있다. 다음의 그래프를 바탕으로 fuel은 thermal, epithermal 영역의 반응을, moderator의 경우 thermal 영역의 반응만 고려하기로 하자.
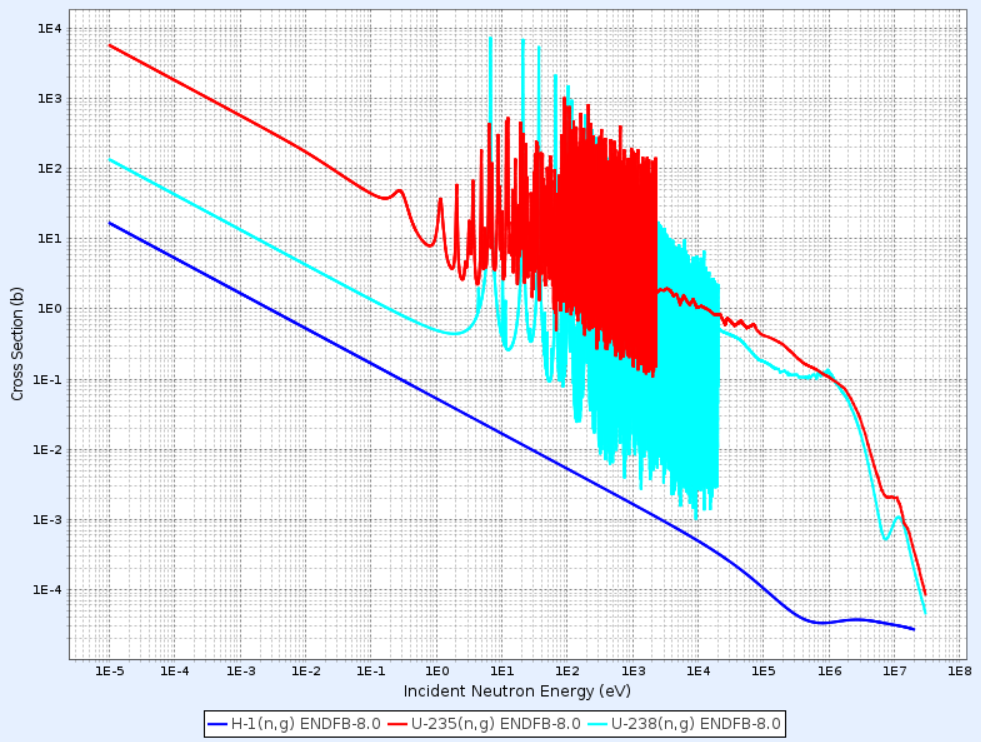
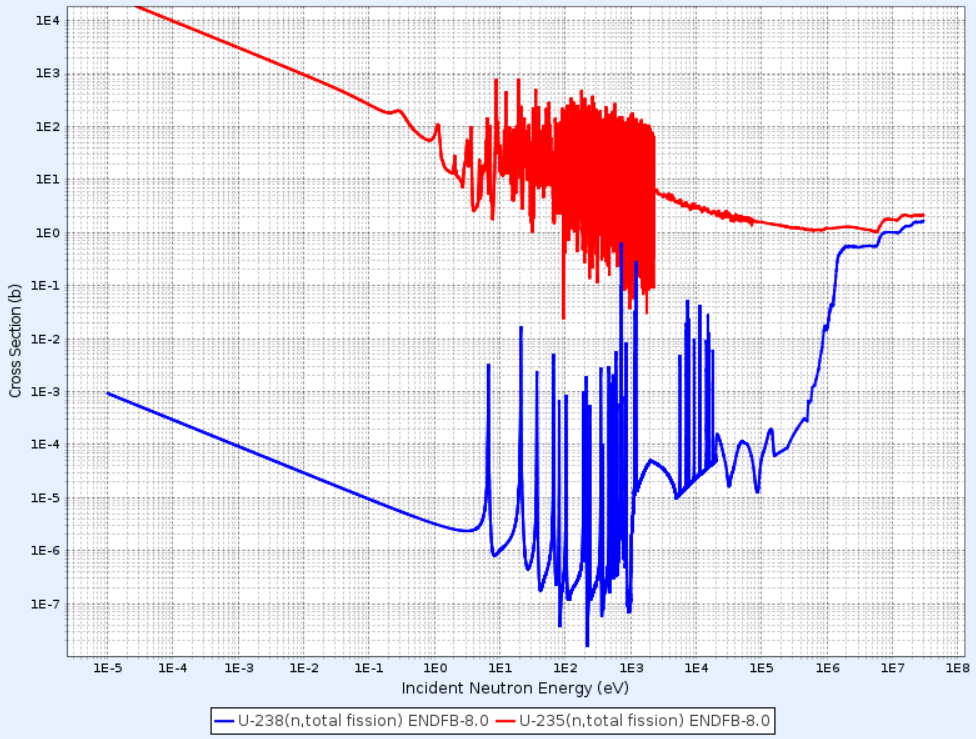
Fission의 경우 U-235는 거의 열중성자 영역에서만 반응하나, 속중성자 영역으로 가면 U-238의 cross section이 증가하여 fission이 발생한다.
따라서 무한증배계수를 근사하면 다음을 얻는다.
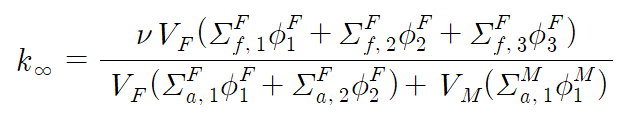
ii. four factors(4인자)
Cell이 무한히 크다는 가정 덕분에, 한 세대마다 중성자 수가 증가하는 비율은 전체 흡수된 중성자 수 대비 전체 생성된 중성자 수로 간단히 나타낼 수 있다. 각각을 대문자 P와 A로 쓰기로 하자.
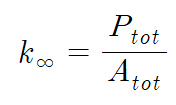
원자로 내의 중성자는 한 세대 동안 여러 단계를 거치는데, 이에 맞춰 무한증배계수는 각 과정에 해당하는 더 작은 계수들의 곱으로 구성되어 있다. 하나의 중성자가 한 세대 동안 지나는 단계들을 살펴보면서 무한증배계수가 어떻게 계산되는지 알아보자.
중성자가 최초로 생성되는 시점은 열중성자 영역에서 U-235의 fission이 발생하는 때이다. U-235에 흡수된 열중성자의 수를 n_0라 두면, 분열당 생성되는 평균 중성자 수만큼의 배율로 중성자 수가 증가한다. 이 배율을 thermal neutron production factor라 하며 thermal 영역에서의 재생계수(reproduction factor)에 해당한다. 이 과정에서 새로 생성된 중성자는 높은 에너지를 가진다.

U-235의 속중성자에 대한 fission cross section은 열중성자에 대한 값보다 훨씬 작지만, 고에너지 영역에서 U-238의 fission cross section이 크게 증가하기 때문에 fission으로 생성된 속중성자가 다시 fission을 일으킬 수 있다. 앞선 그래프에서 확인되는 U-238의 cross section은 충분하지 않은 것으로 보이겠지만, 전체 핵연료에서 U-238이 차지하는 비중이 235에 비해 훨씬 높다는 것을 감안하자.
이처럼 고에너지 영역에서 발생하는 fission으로 인한 증가율을 fast fission factor(속분열인자)라 하고 ε로 표기한다. 모든 fission이 끝나면 중성자는 moderator로 이동하고, 그림으로 나타내면 다음과 같다.
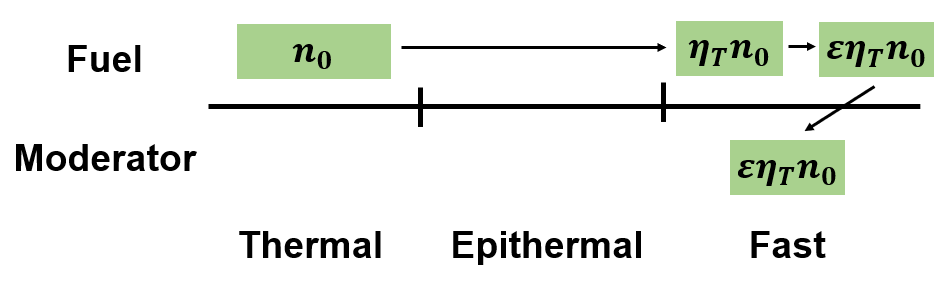
고에너지 영역에 머무르던 중성자들은 곧 moderator와의 scattering을 거쳐 점차 에너지를 잃는다. 일반적으로 absorption cross section은 thermal 영역에서만 유의미한 값을 가지나, resonance에 의해 epithermal 영역에서도 중성자가 흡수될 수 있다. 이러한 손실을 거치고 남은 중성자가 thermal 영역에 도달했을 때의 생존율을 thermal absorption fraction, 또는 resonance escape probability(공명이탈률) p라 부른다.

Thermal 영역에 도달한 중성자들은 이제 absorption을 거쳐 그 중 일부가 fission을 일으킴으로써 한 주기를 마무리한다. 이때 fuel과 moderaotr 양쪽에 모두 흡수될 수 있는데, 원자로에서 사용할 수 있는 중성자는 오직 fuel에 흡수된 중성자뿐이다. 따라서 중성자 수는 그 비율만큼 감소하고, 이를 fuel absorption fraction 또는 thermal utilization factor(열유용인자) f라고 쓴다.
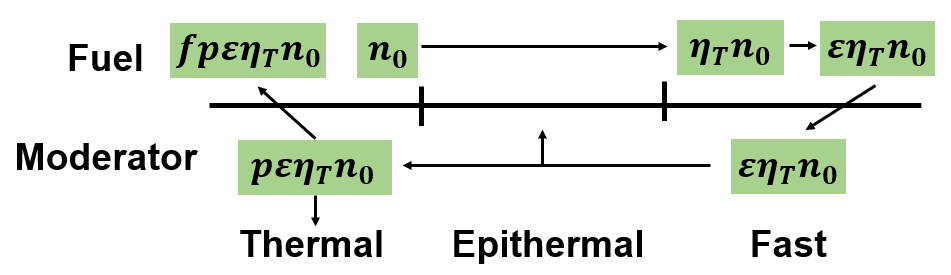
방금 본 세대에서 초기에 생성된 모든 중성자는 무한 조건에 의해 빠짐없이 흡수되었다. 이후 fuel에 도달한 중성자는 그 수에 thermal neutron production factor가 곱해진 만큼의 중성자를 다음 세대에서 새로 생산한다. 따라서 무한증배계수를 계산하면 다음과 같다.

4인자 중 thermal neutron production factor는 핵연료가 갖는 고유한 특성이고, resonance escape probability는 감속재의 특성이다. Fast fission factor의 경우 속중성자가 감속재에 의해 흡수 또는 산란되지 않고 얼마나 남아 있는지에 따라 달라진다.
iii. limitation
실제 cell 환경에서는 중성자가 누출되므로, 실질적인 증배계수 값은 무한증배계수에 비해 작다. 이렇게 계산한 것을 유효증배계수(effective multiplication factor)라 하며, cell 바깥으로 누설되지 않을 확률인 비누설률을 무한증배계수에 곱한 값과 같다.
iv. 경수로와 중수로에서의 무한증배계수
이전 글(seraphy.tistory.com/15)에서 경수로와 중수로의 차이에 대해 간단히 살펴보았다. 중수는 중성자를 흡수하는 능력이 경수에 비해 떨어져, 따로 U-235를 농축함으로써 중성자 수를 늘리지 않아도 원자로가 지속적으로 가동될 수 있다고 하였다. 이번에는 두 원자로 간의 무한증배계수를 비교하고자 한다.

위 표에서 눈여겨볼 것은 PWR(가압경수로)와 PHWR(가압중수로)의 수치이다. 먼저 fast fission factor의 경우, 중수로는 중성자 흡수 능력이 떨어져 열중성자의 수가 매우 많다. 따라서 속중성자의 fission으로 증가하는 비율이 상대적으로 낮은 편이다. 다음으로 resonance escape factor는 cell에서 moderator가 차지하는 비율이 큰 중수로가 더 높은데, 이는 흡수가 잘 되지 않는 중성자들이 넓은 moderator 범위에 주로 머무르기 때문이다. Thermal utilization factor는 차이가 거의 없고, 재생인자의 경우 농축우라늄을 쓰는 경수로 쪽이 더 크다. 이를 종합하면 전체 무한증배계수는 경수로에서 더 크게 계산되는데, 이 때문에 연료를 빠르게 소진하는 관계로 연료 교체 주기가 상대적으로 짧다.
참고문헌
1. Han gyu Joo, "Four Factor Formula(Introduction to Nuclear Engineering 1)", Seoul National University (2020)
2. J. K. Shultis, R. E. Faw, "Fundamentals of Nuclear Science and Engineering", 2nd ed., CRC Press (2008)
3. J. R. Lamarsh, A. J. Baratta, "Introduction to Nuclear Engineering", 3rd ed., Prentice Hall (2001)
4. 이은철, 조건우, 김응수, "핵공학개론", 한티미디어 (2018)
이미지
'핵공학개론1' 카테고리의 다른 글
| [6] 열역학 기초 (0) | 2021.03.15 |
|---|---|
| [5] 원자로 내 중성자 분포 (1) | 2021.02.16 |
| [3] 에너지에 따른 중성자 분포 (1) | 2021.02.07 |
| [2] 중성자 (0) | 2021.01.31 |
| [1] 핵분열 기초 (0) | 2021.01.27 |








