[3] 에너지에 따른 중성자 분포
핵공학개론1 2021. 2. 7. 02:58
0. 서론
이전 글(seraphy.tistory.com/15)에서 중성자의 충돌과 그로 인한 에너지 손실을 설명하던 중 감속재(moderator)에 대해 짧막하게 언급한 바 있다. 감속재는 말그대로 중성자의 속도를 줄여주는 역할을 하는데, 그 이유는 핵연료인 U-235의 fission cross section이 중성자 에너지가 낮은 영역에서 높게 나타나기 때문이다. 이처럼 저에너지의 중성자를 열중성자(thermal neutron)라 부르고, 반대로 고에너지의 중성자는 속중성자(fast neutron)라 한다.
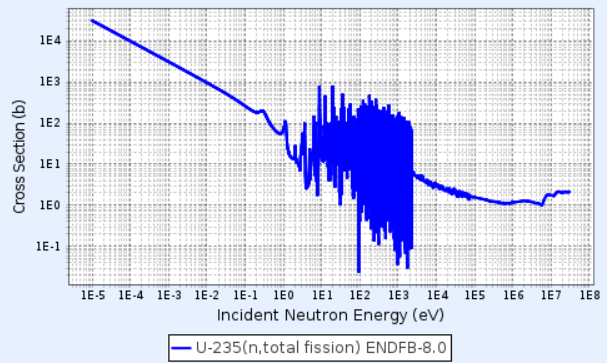
요컨대 U-235를 핵분열에 사용하여 많은 에너지를 얻고자 한다면 낮은 에너지의 중성자 수를 많이 확보하는 것이 중요한 일이 된다. 이 사례에서 볼 수 있듯이, 핵분열에서 중요하게 살펴야 할 조건 가운데에는 cross section뿐만 아니라 특정 에너지를 가진 중성자의 비율, 즉 neutron flux도 포함되어 있다. 실질적인 반응 정도를 보여주는 지표인 반응률(reaction rate)이 macroscopic cross section과 flux의 곱으로 계산되는 것도 이러한 점을 함축한다. 그렇다면 핵분열이 진행 중인 원자로 내부의 중성자는 어떤 에너지 분포를 가지고 있을까?
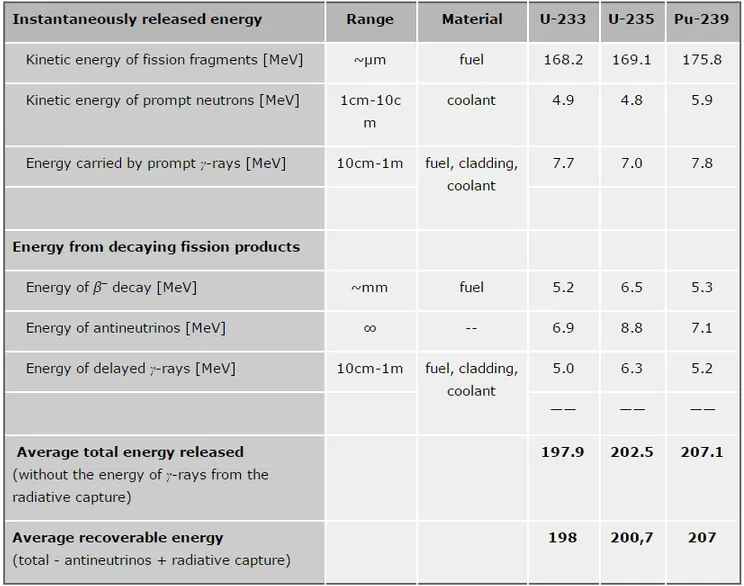
이전 글의 마지막 부분에서 U-235의 핵분열로 얻을 수 있는 에너지 200MeV 가운데 중성자가 가지고 나오는 양은 4.8MeV 정도인 것을 표를 통해 확인할 수 있다. U-235는 분열당 평균 2.4개의 중성자를 방출하므로 개당 운동에너지는 2MeV 수준인데, 이를 그대로 핵분열에 사용하기에는 cross section이 작아 유용하지 않다(위 그래프에서 확인해보자). 따라서 감속재로 사용되는 물질의 핵과 이 중성자를 충돌시켜 scattering을 유도함으로써 충분히 에너지를 감소시키는 과정이 필요하다. 이전 글에서 논하였다시피, 충돌로 에너지를 많이 잃게 하려면 감속재의 질량수는 낮은 쪽이 유리하고, 이에 더해 capture cross section이 매우 작아야 한다. 감속 목적으로 투입한 물질에 중성자가 대거 흡수되어서는 안 되는 일이다.
본 글에서는 이와 같은 과정, 요컨대 핵분열로 생성된 고에너지의 중성자가 scattering을 거쳐 속도가 줄어드는 과정을 모델화하여 중성자의 에너지에 따른 분포를 알아보고자 한다. 이후 이에 따른 반응률을 계산할 것인데, 반응률을 구성하는 두 값 macroscopic cross section과 flux는 에너지에 따라 달라지므로 한쪽을 다른 한쪽의 가중치 삼아 적분하는 방법을 사용하게 된다.
반응률에 대한 설명은 이전의 글에 포함되어 있는 관계로, 링크를 걸어두는 것으로 대신한다.
2020/11/25 - [핵공학개론2] - [1] 플라즈마 개념 정리
I. Neutron Flux
i. reaction rate
Neutron flux는 단위시간당, 단위면적당 입사하는 중성자의 수를 의미한다. 이것을 에너지에 대한 함수로 나타내면 다음과 같다.

위 그래프는 일반적인 중성자 에너지 분포를 나타낸 것으로, 낮은 에너지 영역을 thermal, 중간 에너지 영역을 epithermal 또는 intermediate, 고에너지 영역을 fast로 칭한다. Flux가 thermal 영역에서는 Maxwellian distribution을 따르고, epithermal 영역에서는 에너지에 반비례하며, fast 영역에서는 fission 특성에 따라 결정된다. 전체적으로 열중성자의 수가 압도적으로 많은 것을 확인할 수 있다.
이때 미소에너지가 곱해진 값 Φ(E)dE가 flux의 단위를 갖고, 반응률은 macroscopic cross section과 flux를 곱한 뒤 적분하여 다음처럼 계산한다. i는 혼합물 내의 여러 원소들에 번호를 부여한 것이다.

이때 R_i는 다음과 같다.
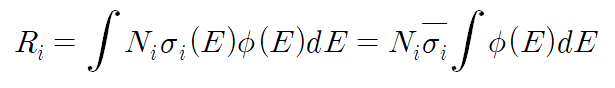

반응 확률이 높아도 중성자 수가 적으면 반응률이 떨어지므로, 이와 같이 가중평균하여 사용하는 것이 적절하다. 이로부터 전체 에너지에 대해 적분한 macroscopic cross section을 다음과 같이 서술하기로 하자.
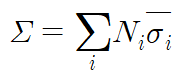
ii. multiplication factor(증배계수)
가중평균한 macroscopic cross section을 사용하는 예를 하나 들기 위해, 증배계수를 계산해보자. 증배계수는 현재 세대에서 생성된 중성자의 수를 이전 세대에서 생성된 중성자 수로 나눈 값을 말한다. 이전 세대에서 생성된 중성자가 핵연료에 흡수되어 핵분열을 일으켜야 중성자가 새로 생성되는데, 그렇게 되지 않고 누설되거나, 핵연료가 아닌 감속재에 흡수되거나, 핵연료에 흡수되었으나 핵분열을 일으키지 못하면 손실로 계산한다.

위 그림은 fuel-moderator cell의 단면을 나타낸 것이다. 중심에는 연료봉이 있고, 그 주위에 간격을 두고 클래딩(피복)이 감싸져 있으며 바깥은 감속재(또는 냉각재)로 채워져 있는 상태이다. 이상적인 조건을 가정하여, 클래딩의 부피를 0으로 두고 cell의 부피를 무한대로 생각하자. 이렇게 하면 클래딩의 존재를 무시할 수 있고, cell 바깥을 향하는 중성자의 누설이 없다고 둘 수 있다. 이때의 증배계수는 생성되는 중성자 수를 흡수되는 중성자 수로 나누어준 값과 같으며, 이를 무한증배계수(infinite multiplication factor)라 부른다.
무한증배계수를 식으로 쓰면 다음과 같다. V는 부피, 첨자 F는 fuel, M은 moderator를 의미하며 f와 a는 각각 fission과 absorption의 약자이다. ν는 반응당 생성되는 중성자의 수를 뜻한다. Absorption은 fuel과 moderator 모두에서 일어나지만 fission은 fuel에서만 발생하는 것에 유의할 것.
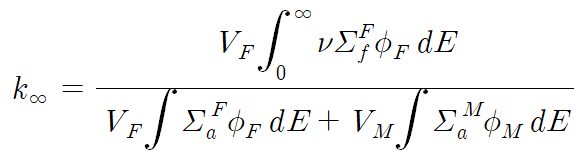
앞 문단에서 썼던 가중평균을 사용해 표현하면 다음과 같다. thermal, epithermal, fast 영역의 번호를 각각 1, 2, 3으로 쓰고, 핵연료는 U-235와 U-238, 그리고 O로 이루어져 있으며 감속재는 물(경수)로 설정하자. 각 원소를 의미하는 우하첨자는 질량수로 표기하였다. O는 absorption에는 관여하나 fission에는 관여하지 않는 것에 유의하자.
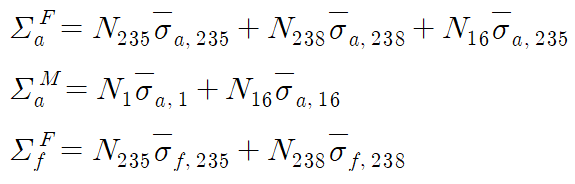
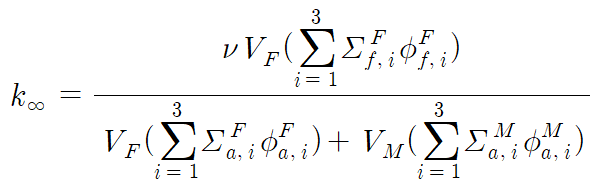
이때 ν는 혼합물을 대상으로 계산한 평균값을 사용한다.
iii. deceleration(in H-1)
에너지에 따라 중성자의 분포를 나타내면, 분열 직후 에너지를 많이 가진 중성자가 주위 핵(주로 감속재)과의 scattering을 통해 점차 에너지를 잃는 전개를 상정할 수 있다. 수소를 감속재로 하는 예시를 들어 이를 수식으로 확인해보자.
임의의 에너지 E에 대해, 총 생성량과 손실량은 항상 같다. fission으로 만들어진 중성자가 해당 에너지 E를 가지는 경우, 그리고 E < E'인 에너지 E'에서 scattering에 의해 에너지가 E로 감소하는 경우가 생성에 해당한다. 손실은 에너지 E에서의 반응률로 계산할 수 있다. 반응률의 단위에 맞춰 단위부피당, 단위시간당 전체 에너지 범위에서 생성되는 중성자의 수를 s_0라 두자. 그러면 식을 다음처럼 쓸 수 있다.
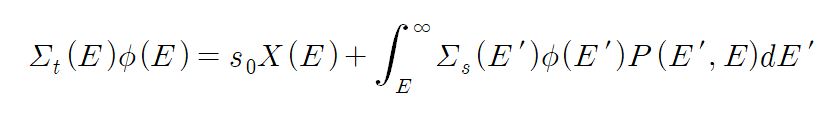
우하첨자는 total과 scattering을 의미하고, P(E', E)는 에너지 E'에서 E로 scattering될 확률을 뜻한다. X(E)는 전체 핵분열 중성자 중 에너지가 E인 비율을 나타낸다.
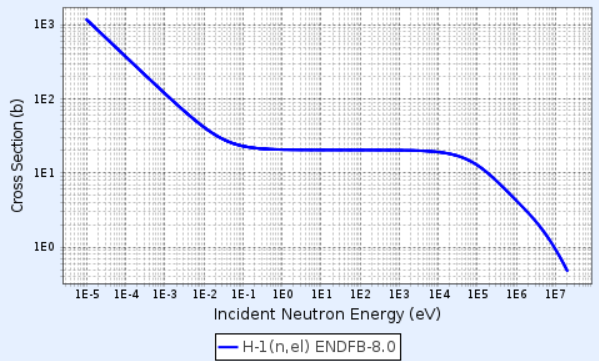
위 그래프는 수소의 (elastic) scattering cross section을 나타낸 것이다. 대략 0.1eV ~ 1e+4eV 구간에 걸쳐 cross section이 거의 일정한 값을 가지는 것을 알 수 있는데, 이를 참고하여 일전의 식에서 scattering cross section을 E'에 독립적인 상수로 가정하자.
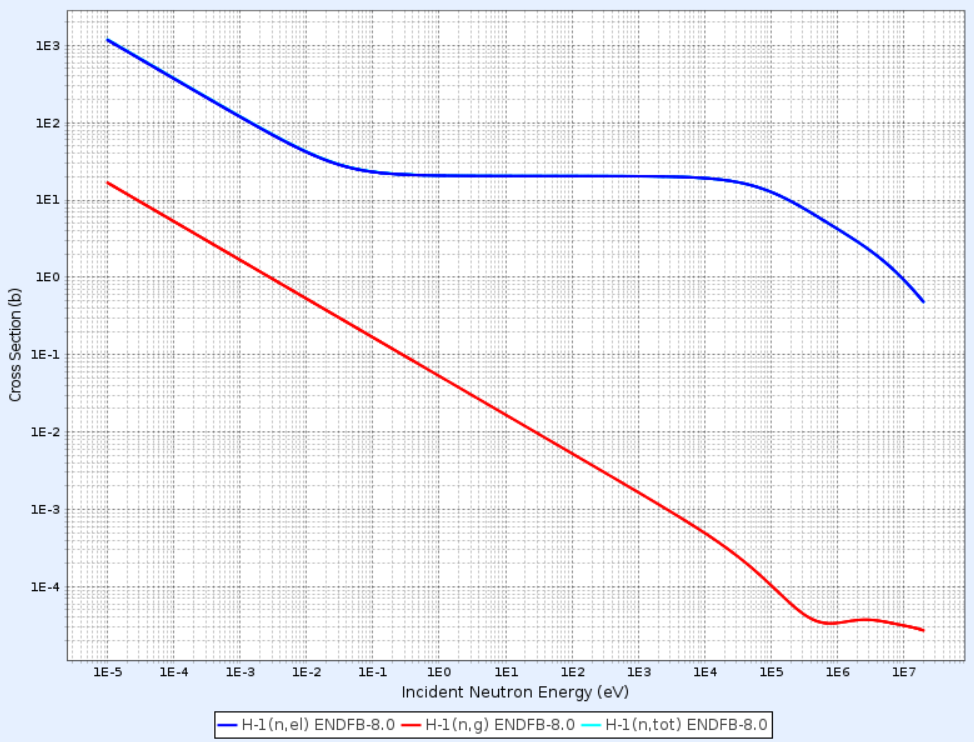
또 수소의 total cross section과 개별 cross section을 비교한 것은 다음과 같다. Elastic scattering이 지배적인 반응이기 때문에 그 cross section은 total cross section과 거의 일치한다.
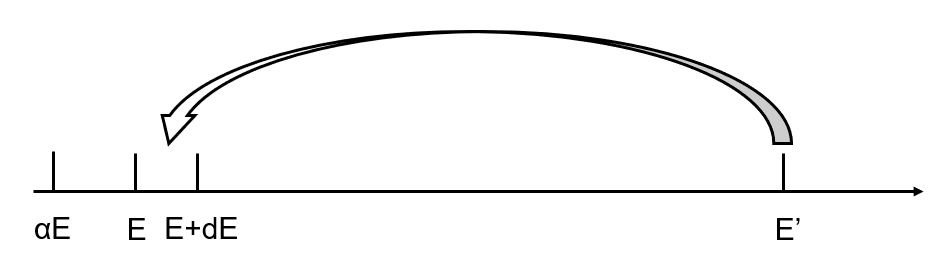
마지막으로 이전 글(seraphy.tistory.com/15)에서 언급된 바에 따르면 scattering에 의해 에너지가 감소하는 과정을 다음 그림처럼 나타낼 수 있다. 임의의 에너지 E'에서 최소 에너지 αE' 사이의 구간 [E, E+dE]로 진입하는 것을 의미한다.
따라서 scattering 확률은 다음처럼 정의된다.
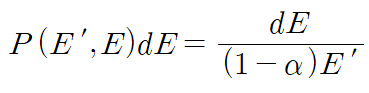
수소의 경우 질량수가 1이므로 α=0이다. 이를 종합하여 앞선 식을 정리하면, flux에 대한 다음의 적분방정식을 얻는다.
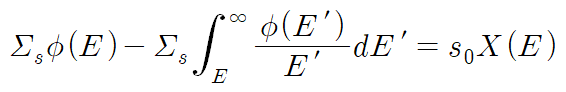
이를 계산하여 다음의 해를 구할 수 있다. 풀이과정은 부록으로 남긴다.
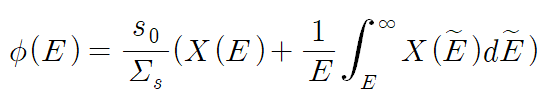
에너지 범위를 fission 중성자가 가질 수 없는 에너지 범위(E < 0.1MeV)로 제한하면 X(E)=0이 되고, E 이상의 범위에서 X(E)를 적분한 값은 1이 된다. 따라서 해당 범위에서는 다음 식이 성립한다.
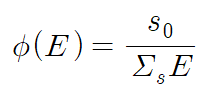
식을 바꾸어, flux와 E의 곱을 대상으로 그래프를 그리면 해당 범위에서 상수로 나타난다. 만약 fission에 의한 생성을 포함하면 fission neutron의 스펙트럼 형태와 유사한 그래프가 나타난다.
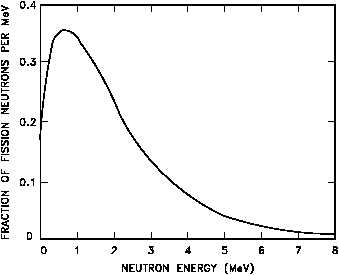
따라서 이상의 논의로부터 다음의 flux spectrum을 그릴 수 있다. y축은 flux에 에너지를 곱한 값이고, x축은 log scale이다. Fission에 의한 중성자 생성이 가능한 에너지 이전에는 일정한 상수 값을 가지다가, 그 이후부터는 fission spectrum을 따라가는 것을 볼 수 있다.
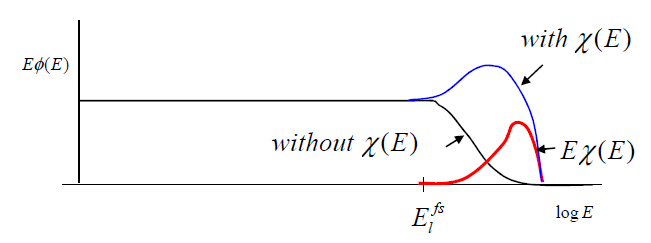
위 spectrum은 본 글의 초기에 등장했던 epithermal 영역과 fast 영역에서의 중성자 flux를 각각 보여준다(y축이 가리키는 값이 달라진 점에 유의할 것).
iv. upscattering과 Maxwell-Boltzmann distribution
그런데 저에너지의 thermal 영역에서는 위 문단에서의 유도를 통해 얻은 spectrum과는 다른 형태의 그래프가 확인된다. 이러한 차이가 발생하는 이유로는 여러 가지를 들 수 있는데, 첫째로 우리가 수소의 total cross section이 elastic scattering cross section과 거의 같다는 가정을 사용했기 때문이다. 이전 글(seraphy.tistory.com/15)에서 중성자의 속력이 낮아질수록 capture가 발생할 확률이 높아진다고 언급을 했었다. 이 때문에 capture cross section이 충분히 커져서 무시할 수 없는 수준이 되는 저에너지 구간에서는 이를 고려하여 flux를 예상할 필요가 있다.
둘째는 capture cross section이 증가할 뿐만 아니라, scattering으로 인해 중성자가 에너지를 계속 잃으면서 저에너지 영역의 중성자 수가 매우 많아진다는 점이다. 요컨대 flux가 E에 반비례한다고 했는데, 이는 극히 낮은 에너지 영역에 존재하는 중성자의 flux를 과대평가한다는 단점이 있다. 따라서 cross section을 flux에 가중평균하여 구한 reaction rate는 thermal 영역에서 유의미하게 커진다.
셋째는 중성자의 속도가 느려지면서 충돌 모델 자체가 성립하지 않게 되었기 때문이다. 우리는 멈춰있는 target에 중성자가 충돌하는 모델을 상정했는데, 중성자가 지나치게 느려지면 더 이상 target의 속도를 무시할 수 없게 된다. 이 때문에 원래대로라면 중성자의 에너지가 target에 단방향으로 전달되는 과정만을 고려했겠지만, 반대로 중성자가 target에 충돌한 뒤 오히려 에너지를 얻게 되는 현상이 발생한다. 이를 upscattering이라 부른다.
이상의 예외를 어떻게 처리할 수 있을까? 세 번째 이유를 잘 들여다 보면, 모든 입자가 각자의 속도로 움직이고 서로 간의 에너지 전달이 활발히 이루어지는 환경을 이미 살펴본 바 있다. 시스템이 열평형 상태에 도달했다고 가정하면 시스템 내의 입자들은 Maxwell-Boltzmann distribution을 따른다는 것이다. 아래 그림은 저에너지의 중성자가 target과의 충돌로 upscattering을 거치면서 Maxwell distribution으로 변해가는 과정을 보여준다.
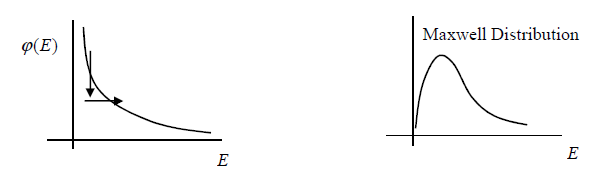
에너지에 대해 나타낸 Maxwell-Boltzmann distribution은 다음과 같다(이와 관련된 내용은 본문 최상단에 링크된 글에 포함되어 있다).
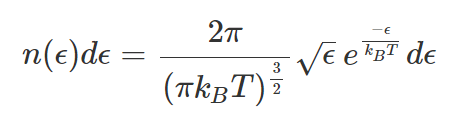
위 식을 따르는 분포는 E=kT일 때 최댓값을 갖는다. 예컨대 293K의 상온에서 열평형이 이루어진 중성자 속도의 최빈값은 약 2200m/s이다.
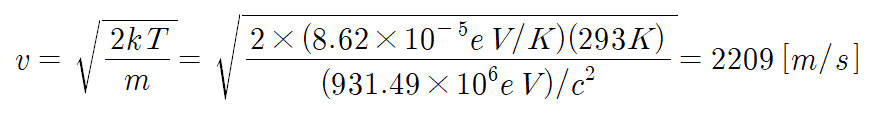
이를 활용해 저에너지 영역에서 중성자의 capture cross section에 가중평균을 취해보자. 간단히 말하자면 thermal 영역의 중성자 flux를 사용해 아래의 값을 구하는 것이다.

이때 flux를 normalize하면 위 식의 분모가 1이 되어 한층 간결해진다. Flux는 확률밀도와 속력의 곱으로 나타나므로 normalize 과정은 다음과 같다. Normalize된 flux를 구별하기 위해 hat 기호를 사용하였다.
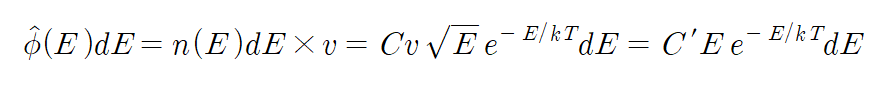
위 식을 전체 에너지 범위에서 적분한 값이 1이 되도록 상수 C'을 구하면 다음을 얻는다. 자세한 계산 과정은 생략한다.
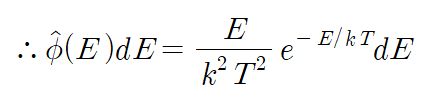
Thermal 영역에서 capture cross section은 속력에 반비례한다. 가중평균한 cross section을 대표할 값으로 Maxwell-Boltzmann distibution의 최빈값을 선택하여 다음과 같이 나타낼 수 있다.
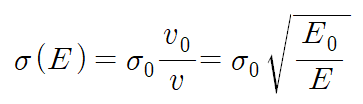
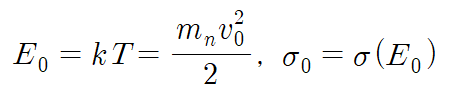
즉, 온도 T에서 열평형이 이루어진 중성자에 대해, 최빈 에너지 kT에서의 capture cross section으로 thermal 영역에서의 flux에 대해 가중평균한 cross section을 표현하고자 하는 것이 이 과정의 목표이다.
Maxwell-Boltzmann distribution은 저에너지 영역에서만 나타나기에 가중평균 시 적분 범위를 thermal-epithermal의 경계 에너지까지로 잡는 것이 원칙이다. 그러나 계산의 간편함을 위해 전체 에너지 범위에 대해 적분하자. 이렇게 해도 Maxwell distribution이 고에너지 영역에서 매우 낮은 값을 갖기 때문에 큰 오차는 발생하지 않는다. 이를 계산하면 다음을 얻는다.

따라서 thermal 영역에서 가중평균한 capture cross section은 열평형 온도에서 측정한 cross section의 0.886배와 같음을 알 수 있다.
v. resonance self-shielding과 leakage
지금까지 다소 긴 분량에 걸쳐 thermal, epithermal, 그리고 fast 영역에서의 중성자 flux를 살펴보았고, 이들을 이용해 reaction rate나 cross section을 가중평균하는 방법을 설명하였다. 마지막으로 epithermal 영역에서 발생하는 현상 두 가지를 언급하고 본 글을 마무리하고자 한다.
Fission의 대부분을 담당하고 있는 U-235는 주로 열중성자와 반응한다고 앞서 언급하였다. 그러나 핵연료 내에는 U-235 외에 U-238이 다수 포함되어 있고, 이들은 capture 반응을 일으킨다. 다만 U-235의 capture 반응보다도 그 확률이 낮은 편인데, 간혹 resonance에 의해 U-238에 의한 capture가 flux에 유의미한 영향을 주기도 한다.
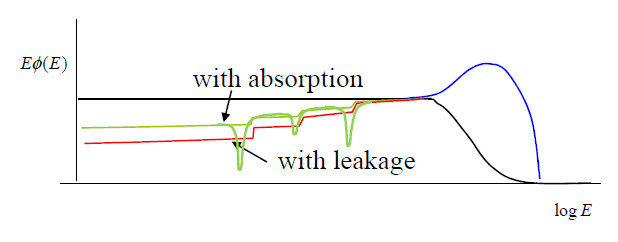
위 그래프에는 resonance에 의해 U-238이 중성자를 흡수하여 flux가 대폭 감소하는 모습이 나타나 있다. 일반적으로 핵연료 내에서 U-238의 밀도는 중성자의 밀도보다 높아 capture cross section이 증가할 때마다 중성자 수는 급격히 감소하게 되는데, 이 때문에 다른 핵은 거의 중성자와 반응하지 못한다. 이러한 현상을 resonance self-shielding effect라 부른다.
또한 scattering 과정에서 지속적으로 발생하는 leakage도 flux를 감소시키는 요인 중 하나이다. 이러한 요인들이 종합적으로 영향을 미쳐, 중성자 flux는 위에서 구한 이론값보다 복잡한 양상을 보인다.
부록 : 적분방정식의 계산

참고문헌
1. Han gyu Joo, "Neutron Moderation and Spectra(Introduction to Nuclear Engineering 1)", Seoul National University (2020)
2. Han gyu Joo, "Four Factor Formula(Introduction to Nuclear Engineering 1)", Seoul National University (2020)
3. J. K. Shultis, R. E. Faw, "Fundamentals of Nuclear Science and Engineering", 2nd ed., CRC Press (2008)
4. J. R. Lamarsh, A. J. Baratta, "Introduction to Nuclear Engineering", 3rd ed., Prentice Hall (2001)
5. 이은철, 조건우, 김응수, "핵공학개론", 한티미디어 (2018)
6. indico.ictp.it/event/a04183/session/56/contribution/32/material/0/0.pdf
이미지
3. www.researchgate.net/figure/Unit-cell-model-of-PWR-UO-2-fuel_fig1_282801195
'핵공학개론1' 카테고리의 다른 글
| [6] 열역학 기초 (0) | 2021.03.15 |
|---|---|
| [5] 원자로 내 중성자 분포 (1) | 2021.02.16 |
| [4] 4인자 공식(Four Factor Formula) (0) | 2021.02.12 |
| [2] 중성자 (0) | 2021.01.31 |
| [1] 핵분열 기초 (0) | 2021.01.27 |








