[7] 원자로 내 열 전달
핵공학개론1 2021. 7. 2. 16:000. 서론
노심은 간단히 나누어 연료봉(fuel)과 냉각재(coolant)로 구분된다. 원자로 코어를 구성하는 기본 단위인 cell은 가운데 자리잡은 원통형의 fuel과 그 주변을 채운 coolant로 이루어져 있고, 이러한 사각형 cell이 무수히 모여 원자로에 열을 공급하는 역할을 한다. 연쇄반응이 일어날 조건을 만족한 원자로에서는 핵분열을 통해 fuel에서 방출된 열이 coolant를 타고 이동하며, 그 에너지를 사용해 발전기를 돌린다. 이러한 과정을 살펴보기 위해 원기둥의 연직 방향 축을 기준으로 한 heat flux를 알아보고, 그것이 coolant로 전달되는 양을 계산할 것이다.
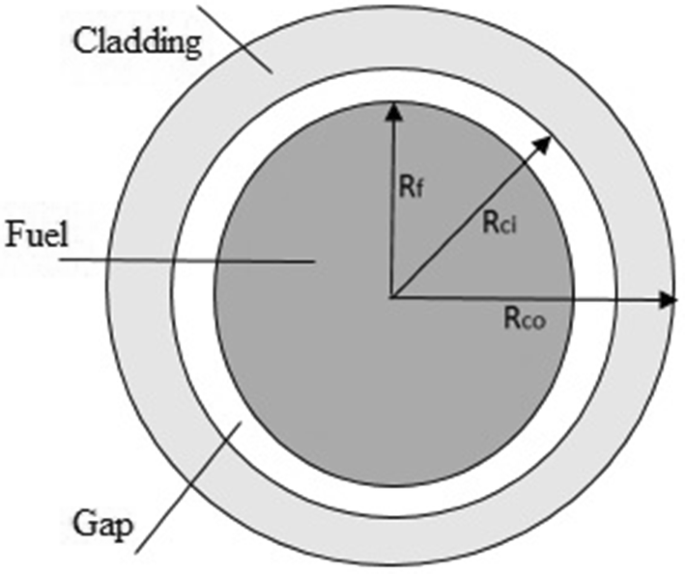
또한 연료봉은 연료에 해당하는 pellet을 지르코늄 등의 재료를 사용한 피복(cladding)이 감싸고 있는 형태로 제작되었으며, 이 둘 사이에는 좁은 빈 공간(gap)이 존재한다. 내부에서부터 차례대로 pellet, gap, cladding, coolant의 순서로 나열되어 있는 radial 방향의 구조에서 각 위치에서의 온도를 아는 것은 핵연료 안전성을 평가하는 데에 필수적인 요소이다. 예를 들어 cladding이 있는 영역의 온도가 cladding의 녹는점에 도달한다면 해당 설계는 안전하지 않다. 이 구조에 대한 열전달 방정식을 세우고 풀이하면, 중심에서 시작해 점차 감소해가는 온도 분포를 얻을 수 있다.
1. 열의 이동
i. 개념 정리(열량, 엔탈피, 비열)
지난 글(https://seraphy.tistory.com/19)에서 이상기체 상태방정식을 구성하는 4개의 인자로 압력, 부피, 몰 수와 온도를 알아보았고, 이 값의 모음을 사용해 열역학적 상태가 표현될 수 있음을 확인했다. 열역학 제1법칙은 어떤 이상기체가 상태 A에서 상태 B로 변할 때, 상태함수인 내부에너지 U의 변화량과 경로함수로 주어지는 기체가 받은 일 W를 조합하면 계에 출입한 열량 Q를 계산할 수 있음을 보여준다.
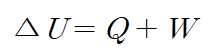
W의 정의에 따라 물리학에서, 또는 화학에서 식의 형태가 다른 경우가 종종 있다. 일은 PV의 변화량으로 정의되는데, 기준을 기체가 받은 일로 정할지, 한 일로 정할지에 따라 W와 부피 변화량 ΔV 사이의 관계가 달라진다. 본 글에서는 기체가 외부로부터 받은 일로 정의하였으므로, W와 ΔV의 부호는 서로 반대로 정한다.
위 식에는 내부에너지의 변화량을 계에 출입한 열량과 일의 합으로 표현하고 있는데, 열의 이동을 관찰하는 입장에서 열량 Q에 더 집중하고자 하는 생각을 해볼 수 있다. 이를 위해 새로운 개념인 엔탈피(enthalpy) H를 다음과 같이 정의하자.

열역학에서 다루는 문제들 중 몇몇 경우에서는 압력이 거의 일정하게 유지된다. 이후 살펴보겠지만 원자로 내 유체에서 등압조건이 성립하며, 이 경우 엔탈피의 변화량은 계에 출입한 열량과 같다.

요컨대 계에 출입한 열량을 어떤 물리량의 변화량으로써 나타내기 위한 목적으로 엔탈피를 정의한 것이다. 위 식처럼 대문자로 표기된 값은 단위가 J이고, 만약 h나 q처럼 소문자로 쓴다면 그것은 specific value(J/kg)를 의미하며, 단위질량에 대한 물리량을 뜻한다.
우리가 열량을 알아야 하는 가장 큰 이유는 열량의 흐름이 특정 위치에서의 온도를 계산하는 데에 쓰이기 때문이다. 어떤 물체에 열량을 공급하는 것을 가열이라 부르며, 온도의 변화량은 물체에 공급한 열량에 비례한다. 이때의 비례상수를 비열(specific heat)이라 하고, 비열은 물질의 고유한 특성에 해당한다. 열량과 온도 간의 관계식은 다음처럼 주어지는데, 여기서 비열은 온도의 함수이다.

우하첨자 p는 등압조건에서의 비열을 의미한다. 외부에서 주어진 열량이 온도로 대표되는 물체의 내부에너지로 전환되는 과정은 곧 물체를 구성하는 입자의 열운동이 심화되는 것과 같은데, 이때 개별 입자가 움직일 수 있는 양상이 다양할수록 물체는 같은 온도 증가량에 대해 더 많은 에너지를 흡수할 수 있다. 이를 자유도(degree of freedom)라 하며 이 때문에 등압과정과 등적과정에서의 비열은 서로 다르다. 본 글에서 자유도와 비열에 대한 더 이상의 설명은 하지 않는다.
따라서 엔탈피와 온도 간의 관계식은 다음과 같이 정리된다.

ii. 열 전달 방정식
이전의 글(https://seraphy.tistory.com/18)에서 입자가 단위시간당, 단위면적당 이동하는 것을 flux라 정의하고, Fick's law와 같이 밀도의 그라디언트로 이를 표현했던 것을 기억할 것이다(참고로 시간을 고려하지 않은 단위면적당 물리량은 flux와 구분하여 fluence라 부른다). 요컨대 특정 지점에서 측정할 수 있는 물리량을 단위거리, 단위면적, 단위시간 등에 대해 표현하면 이는 해당 물리량의 흐름을 의미하는 새로운 개념으로 생각할 수 있다. 열에 대해 이 방법을 적용해 heat flux를 다음처럼 정의할 수 있을 것이다.
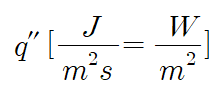
q에 첨가된 프라임의 개수는 차원을 나타낸다. 예컨대 위 식처럼 2개를 적으면 단위면적당이고, 3개를 적으면 단위부피당으로 해석하면 된다.
열의 전달 방법에는 전도, 대류, 복사가 있다. 원자로 내에서 주로 다루는 것은 앞의 두 가지로, 각각 푸리에의 열 전도 법칙(Fourier's law of heat conduction)과 뉴턴의 냉각 법칙(Newton's law of cooling)이 이 현상들을 설명한다.

이때 k와 h를 각각 열 전도율(heat conductivity)과 열 전달계수(heat transfer conefficient)라 부른다.
서론에서 살펴본 원자로 내 구성을 생각해보면 열량은 기체(gap), 액체(coolant)와 고체(fuel, cladding) 상태의 물질을 타고 움직인다는 것을 알 수 있다. 앞서 정의한 specific enthalpy를 사용하면 공급되는 열량과 매개물질의 엔탈피 변화를 연관지을 수 있다.
먼저 유체의 지배방정식을 세워보자. 크게 질량 보존, 에너지 보존, 운동량 보존을 생각해볼 수 있을 것인데, 보존방정식의 기본 형태는 중성자 확산방정식에서 한 번 다룬 적이 있다. 어떤 물리량의 시간변화율은 생성과 손실, 유출과 유입을 조합하여 구한다는 것이었다. 유출과 유입은 outflow로 묶어서 표현할 수 있다.
(rate of change) = (generation) - (loss) - (net outflow)
이 중 net outflow의 경우 current의 발산과 물리적 의미가 같다.
위의 기본 형태를 틀로 두고, 다루고자 하는 물리량을 각 항에 맞게 정의해주면 보존 방정식을 간단히 만들어낼 수 있다. 예를 들어 질량 보존 방정식은 다음처럼 쓸 수 있다.

ρ는 유체의 밀도이고, net generation Γ는 생성량에서 손실량을 뺀 것을 하나로 합쳐 표현한 것이다.
다음으로 에너지 보존 방정식을 세워보자. 가운데에 연료봉을 낀 고리 모양의 유체 기둥을 생각한다. fuel에서 방출되는 모든 열량은 유체에 흡수되며, 유체로부터의 손실은 무시한다. 이 경우 엔탈피의 변화량이 열량이므로 유체의 밀도에 specific enthalpy를 곱한 것이 전체 에너지, 그것의 시간변화율이 열량에 해당할 것이다. 총 에너지 생성량은 이것과 단위를 맞춰 해당 지점에서의 공급 열량 flux인 q'''와 fuel에서 오는 flux의 합으로 둔다. Enthalpy current는 질량 보존에서 살펴본 mass current에 specific enthalpy를 곱한 것과 같고, 따라서 아래의 식을 얻는다.

q''는 fuel(cladding)과 유체의 경계면에서 흐르는 heat flux이고, ζ는 fuel의 둘레로 heat flux가 방출되는 경계면의 길이이다. A_c는 밑면에서 바라본 유체의 전체 면적으로, 이를 종합한 우변의 두 번째 항은 fuel의 열량에 의한 유체 전체 부피에서의 평균 heat flux와 같다.
마지막으로 운동량 보존을 생각해보자. 운동량의 시간변화율은 질량과 가속도의 곱이므로 힘과 같음을 알 수 있다(따라서 운동방정식과 같다). 유체가 받는 힘은 중력과 압력이 있으며, 그 외에는 질량 보존에서와 같은 방식으로 식을 세울 수 있다. 운동량을 기본 물리량으로 하고 있으므로 운동량의 current는 텐서 형식으로 써야 한다.

이제 고체에서의 전도방정식을 세워보자. 유체에서와 달리 고체는 압력에 의한 부피 변화가 매우 적어 엔탈피를 쓰는 것에 큰 효과가 없다. 따라서 내부에너지를 기준 물리량으로 하여 보존 방정식을 쓰면 다음과 같다.

이때 고체에서의 등압/등적조건에 의해 엔탈피는 내부에너지와 같으므로, 앞서 언급된 비열에 대한 식과 푸리에 법칙을 사용하면 다음을 얻는다. 비열에 밀도를 곱해주면서 등장한 대문자 C는 열용량(specific heat capacity)을 의미한다.

또한 고체는 흐르지 않으므로, 질량이나 운동량에 대한 식을 세울 필요가 없다.
2. Steady-State Heat Transfer
열 전달 방정식을 푸는 이유는 결론적으로 전체 원자로의 온도 분포를 알아내기 위함이다. 우리는 열량과 엔탈피를 연관지은 방정식을 위에서 살펴보았고, 각 지점의 엔탈피를 구하면 이로부터 내부에너지, 즉 온도를 계산할 수 있다.
원자로의 fuel이 원통형이라는 점 때문에 일반적으로 원통좌표계를 사용하여 수식을 푼다. 다만 theta 방향으로의 계산은 대칭성을 가정하여 배제하고, axial(z) 방향과 radial(r) 방향에 대해서만 고려한다. 이 두 가지 경우는 유체(coolant)가 그 방향으로 흐르는지의 여부에서 차이를 보인다.
i. axial fluid
원자로 내의 fuel은 열을 공급하고, 아래에서 위를 향하는 방향으로 coolant가 흐르면서 이 열을 가져간다. 유체 흐름을 중력의 반대로 잡은 이유는 만에 하나 과열이 발생해 coolant가 기체로 변할 경우를 대비한 것으로, 밀도 차로 인해 기체가 위로 올라가는 성질을 고려한 것이다. 기체가 되면 열을 충분히 가져가지 못해 노심에 손상이 갈 수 있는데(partial film boiling), 아래로 coolant가 흐르고 있다면 기체는 이에 역행해 올라가므로 노심에서 빠져나가는 데 걸리는 시간이 늘어난다. 이상 상황에서 신속히 벗어나기 위한 설계에 해당한다.

노심의 해석은 이러한 fuel-coolant 구조를 여러 개의 node로 분할하여 진행된다. Node의 개수는 분석하고자 하는 해상도에 따라 다르게 설정할 수 있다. steady-state에서, coolant의 mass flux는 각 node에서 일정하게 유지될 것임을 예상할 수 있고, 따라서 질량 보존은 다음처럼 표현된다. 이때 연직 방향은 z축으로 둔다.

우변을 주목하면, mass flux의 z축 상에서의 변화량이 0이라는 것을 안다(즉, 상수값으로 정해진다). 이를 사용해 에너지 보존을 풀자. 공급되는 총 heat flux를 q'''로 축약하면 식을 다음처럼 쓸 수 있다.
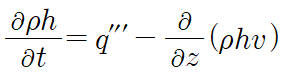
각 node를 지나면서 발생하는 엔탈피의 변화를 알아보기 위해 양변을 i-th node에 해당하는 구간 [z_i-1, z_i]에서 적분한다. 이때 steady state를 가정했기 때문에 시간에 대한 변화는 0이 되고, 앞서 질량 보존에서 mass flux가 상수임을 보였으므로 위 식은 아래와 같이 변하여 간단히 풀린다.

우변의 q_i는 i-th node에서 평균낸 heat flux를 의미한다. 요컨대 node를 하나 통과할 때마다 coolant에 heat flux가 누적되는 과정을 거쳐 엔탈피가 증가하는 것을 알 수 있다. 아래는 위 식의 양변을 상수값인 mass flux로 나눈 것이다.

실제 노심해석 시에는 node의 중간 지점을 엔탈피 이산 분포의 기준점으로 삼는다. 이때 해당 위치에서의 엔탈피는 일반적으로 하단과 상단에서 계산된 엔탈피의 평균값을 사용한다.

이전 글(https://seraphy.tistory.com/18)에서 유한원주 원자로에서의 중성자 분포를 살펴본 바 있다. z축 방향으로는 cosine 형태의 flux가 나타난다고 하였는데, 핵분열에 의해 발생하는 열은 중성자 flux에 비례하므로, 위 식으로부터 엔탈피는 그것의 적분과 유사한 그래프를 가질 것을 예상해볼 수 있다. 단, cosine 함수가 0이 되는 지점은 정확히 구간의 양끝이 아니라 외삽거리를 두고 주어진다(이를 chopped cosine이라 한다).
ii. radial solid
고체에서의 열 전달 방정식은 열용량을 사용한 것이었다. 먼저 열이 생성되는 유일한 영역인 pellet에 대해 살펴보자. 원통좌표계에서의 델 연산자를 대입하고, 마찬가지로 steady state 조건을 적용하면 다음을 얻는다.

q'''를 넘기고 양변을 적분해주면 온도에 대한 식을 얻는다.

즉, 고체에서는 중심에서 멀어질수록 이차함수의 형태로 온도가 감소하는 것을 알 수 있다. 이상의 계산 과정에서 단위부피당 열 생성량 q'''가 상수라고 두었음을 기억하라. 실제로는 중성자 flux와 핵연료 구성비, cross section에 따라 열량이 달라지기 때문에 위처럼 간단한 계산으로는 정확한 답을 얻기 어렵다.
다른 하나의 고체인 cladding에서는 열이 생성되지 않는다. 따라서 생성을 없애고 풀면 아래 식이 나온다.

이는 cladding의 반지름 범위에서 성립하는 식이다. 위 식의 좌변을 살펴보면 그것이 푸리에 법칙에서 나온 것임을 알 수 있는데, 요컨대 좌변 전체가 cladding 구간 내 임의의 위치에서의 heat flux와 같다. 그런데 steady state이므로 pellet에서 나온 모든 열은 cladding을 타고 바깥으로 방출되어야 하고, 따라서 앞선 문단에서 구한 온도에 대한 공식을 가져와 위 식의 우변에 등호로 연결해줄 수 있다.

위 식의 양변을 cladding의 반지름 구간에서 적분하면 다음처럼 로그 형태로 감소하는 온도 공식을 얻는다. r_ci는 cladding inner radius를 나타낸다.

iii. radial fluid
유체에서는 대류에 대한 뉴턴의 법칙이 적용된다. Gap 양쪽 경계의 온도는 (ii) 문단에서 구한 온도 공식으로부터 계산할 수 있는데, gap에서의 온도 강하를 gap의 특성으로 나타내보자.

Gap의 폭이 매우 작다고 두면, 그때의 heat flux는 pellet에서 오는 flux와 같다. 이번엔 푸리에 법칙으로부터 이 flux를 계산해낼 수 있다.
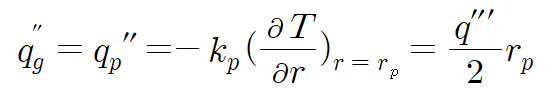
따라서 gap 구간에서의 온도 강하는 다음처럼 쓸 수 있다.

Coolant에서의 온도 강하도 같은 방식으로 구할 수 있다. 이때는 heat flux 대신 단위길이당 열의 총량이 같다고 둠으로써 coolant 구간에서의 flux 변화를 고려해준다.
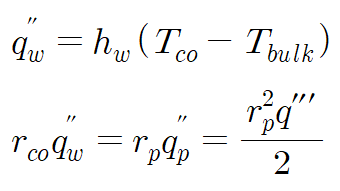
결과적으로 다음 식을 얻는다.

iv. 정리
이상의 식으로부터 fuel 중심과 bulk 사이의 온도 차를 계산할 수 있다.

이때 위 식을, pellet 경계에서의 단위길이당 출력이 제 형태를 갖도록 다음처럼 변형해보자.
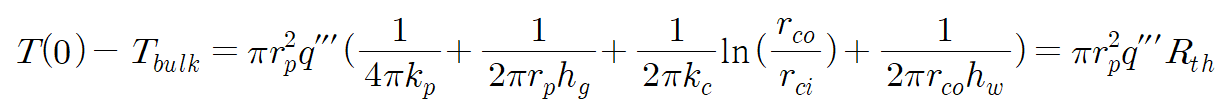
위 식은 pellet의 출력과 온도 강하 정도 간의 선형관계를 보여준다. 우변의 R_th은 열저항이라 하여, 출력 대비 온도 감소가 얼마나 발생하는지를 나타내는 지표에 해당한다.
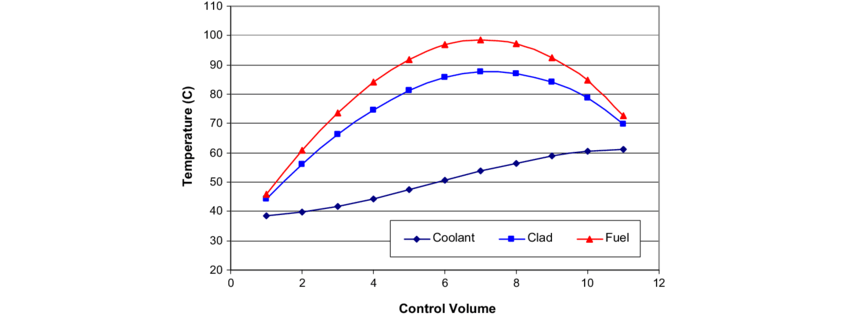
(i) 문단에서 chopped cosine 형태로 axial 방향의 출력이 주어지면, 온도는 그 적분인 sine 형태로 나타난다고 언급한 바 있다. Coolant에 대해 계산한 이 온도를 T_bulk로 잡고, 위 식을 사용하면 전체 fuel에서의 온도 분포를 확인할 수 있다.

참고문헌
1. Han gyu Joo, "Heat Removal form Nuclear Reactors(Introduction to Nuclear Engineering 1)", Seoul National University (2020)
2. J. K. Shultis, R. E. Faw, "Fundamentals of Nuclear Science and Engineering", 2nd ed., CRC Press (2008)
3. J. R. Lamarsh, A. J. Baratta, "Introduction to Nuclear Engineering", 3rd ed., Prentice Hall (2001)
4. 이은철, 조건우, 김응수, "핵공학개론", 한티미디어 (2018)
이미지
'핵공학개론1' 카테고리의 다른 글
| [9] 원자로 내 반응도 피드백 (0) | 2021.08.15 |
|---|---|
| [8] 원자로 동특성(Reactor Kinetics) (1) | 2021.08.08 |
| [6] 열역학 기초 (0) | 2021.03.15 |
| [5] 원자로 내 중성자 분포 (1) | 2021.02.16 |
| [4] 4인자 공식(Four Factor Formula) (0) | 2021.02.12 |








